“

A journey of a thousand miles begins with a single step.

~ Lao Tzu

While one of the aims of this course is to help you develop into an awesome computer scientist, there is also a larger goal. As you learn more about computer science and as you tackle larger and larger problems and programs, we hope that you start to develop stronger and stronger problem-solving skills.

This doesn’t simply mean getting better at finding solutions. It means getting better at engaging in the process of finding solutions. Does that make sense? Maybe not.  Let’s take a closer look…

Imagine that you have a very difficult problem to solve. Maybe it’s developing the culminating task in this course, or maybe it’s cooking dinner for your whole family, or maybe it’s improving an aspect of your community or school.  Just imagine a very difficult problem.

Rather than simply brainstorming possible ideas and then picking the best one, it might be a better idea to use one of the following problem-solving strategies:

If you were building a bridge, the trial and error method might not be the best. The materials and time it would take for each trial would be large, and if an attempt failed it would be disastrous. (If you want to become a bridge builder, promise not to use this method, or at least let everyone know which bridges you’re building.)

Modular Programming

In this activity, you are going to get a chance to combine all three of these problem solving techniques (trial and error, stepwise refinement and divide and conquer) as you learn all about modular programming!

Modular programming involves breaking up large programs into smaller steps. In modular programming, the programmer not only imagines different parts of the program, but he or she programs the parts in separate chunks or blocks.

The following video will take you through some of the big picture ideas behind modular programming. Again, don’t worry about the details such as the syntax, where the code goes, etc. Just watch in order to see how the programmer creates a modular program.

Let’s break down some of the components of the video above in order to get a better idea of how to write modular programs.

The following program prompts the user to enter two numbers. It then adds the two numbers and outputs the sum, and also multiples the two numbers and outputs the result.

package temp2;

import java.util.Scanner;

public class Temp2 {   

    public static void main(String[] args) {

        Scanner keyedInput = new Scanner (System.in);    

        int num1, num2, sum, product;    

        System.out.println("Enter the first number:");
        num1 = keyedInput.nextInt();       

        System.out.println("Enter the second number:");
        num2 = keyedInput.nextInt();         

        sum = num1 + num2;
        product = num1 * num2;       

        System.out.println("The sum is: " + sum);
        System.out.println("The product is: " + product);

    } 

}

In the programmer’s mind, this program is probably divided into chunks. They are probably thinking:

While the programmer can divide the program up a bit in his or her mind, he or she can also divide it up as it is being programmed, by creating blocks or chunks of code that look after specific components. The blocks or chunks can then be combined, and it results in an efficient, well-organized program.

The programmer can create a main program that will prompt the user for the numbers, but then the adding and multiplying will be done in subroutines.

The following interactive shows you the source code that implements two subroutines to complete the project. Rollover the different parts of the project to learn more.

methodDefs

Long Description

The following image will help you review some of the terms involved in creating subroutines in Java.

Now take a closer look at the actual subroutine and its components:

methodsDefs2

Long Description

At this point you might be wondering what happens to program control as subroutines are executed. Which line is executed first? Which line is executed second? Which line is executed last?

The following interactive will take you through a few examples that demonstrate what is happening when you use subroutines in your programs:

methodDefs3

Long Description

Parameters versus Arguments

Remember in the last activity when you talked about parameters and arguments? You use the word parameter when you are writing the definition of the subroutine. You use the word argument when you are talking about the actual method call.

On line 7 above, n1 and n2 are the parameters of type int, written in the definition of the method addAndOut. On line 31, addAndOut is called passing num1 and num2 as arguments to the method.

Passing Arguments

In the interactive above, you may have noticed how the main program used variables num1 and num2, but the subroutines used variables n1 and n2. What exactly was going on here? At this point you might be wondering what happens to program control as subroutines are executed. Which line is executed first? Which line is executed second? Which line is executed last?

On line 31, the main program passes the values of num1 and num2 to the subroutine as arguments. The subroutine then “takes” these values and stores them temporarily in n1 and n2.

When the subroutine is done executing, and program control goes back to the main program, and n1 and n2 disappear and no longer exist. They are only in existence while the subroutine is being executed.

 

Procedures versus Functions

The addAndOut and multAndOut subroutines that you just created are sometimes referred to as procedures. They perform a task, but they don’t return any data back to the main program, and therefore, they return void.

Functions, however, perform a task and also return data back to the main program. To do so, a return type needs to be specified and a return statement needs to conclude the subroutine.

In Java, you use the word "methods" as an umbrella term to include both procedures and functions.

The following video is the same one that you watched at the beginning of this activity. Rewatch it in order to solidify some of these concepts:

Did you notice in the video how the addTwoNums and multTwoNums methods returned values back to the main program?

This was done by:

1. specifying the return type in the method definition:

2. including a return statement in the method:

3. having the ability to receive the data in the main program (in this case, the method call was within an output statement so the data that is returned is output immediately to the screen):

Quite often you might not want to output the data that is returned by a method. Instead, you might want to store it within the main program and use it later.  In this case, you would need to ensure that you have a variable of the correct type, waiting to store the returned data:

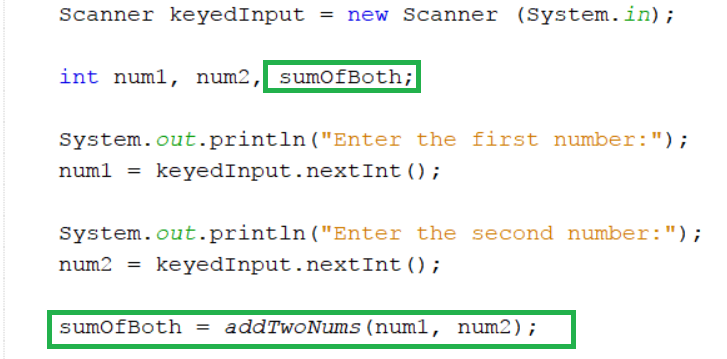
Ordering Parameters

So far, the subroutines that you have created have all used the same type of parameters. As an example, the multTwoNums subroutine required two integers:

It is possible to create procedures or methods that receive more than just two parameters. It is also possible for a procedure or method to receive a variety of parameter types.

The program below prompts users to enter in some information about themselves. The program then uses a procedure to output the data in a user-friendly, well-formatted message:

Notice how there are four different types of parameters that are declared to the subroutine? So when dataOutput is called, the data passed as arguments need to be passed in the same order.

The order is established by the subroutine definition. In this case it’s String, String, integer, double.

Questions

 

1. A programmer wants to create a method that is called subTwoNums. The method receives two integers as parameters, subtracts one from the other, then returns the difference to the main program as an integer.

   Which of the following method definitions is correct?

   1. public static void subTwoNums (int num1, int num2)
   2. public static int subTwoNums (int num1, int num2)
   3. public static int subTwoNums (int num1)
   4. public static double subTwoNums (int num1, int num2)
   Answer

   b. public static int subTwoNums (int num1, int num2)

2. A programmer wants to create a method that is called doesItQualify. The method receives a string and two doubles (in that order) and returns a Boolean value back to the main program.

   Which of the following method definitions is correct?

   1. public static void doesItQualify (String word, double num1, double num2)
   2. public static boolean subTwoNums (String word, double num1 & num2)
   3. public static boolean subTwoNums (double num1, double num2, String word)
   4. public static boolean subTwoNums (String word, double num1, double num2)
   Answer

   d. public static boolean subTwoNums (String word, double num1, double num2)

3. A programmer has created the following method:

   Name: secretCalculation
   Input/Parameters: integer, integer, double
   Output/Returns: double

   In the main program, the following code has already been written:
     int num1 = 4;
     int num2 = 67;
   
     double num3 = 54.87;
     double num4;

   Which of the following method calls to secretCalculation will work?

   1. num4 = secretCalculation (num3, num1, num2);
   2. num2 = secretCalculation (num4, num2, num3);
   3. num4 = secretCalculation (num1, num3, num2);
   4. num4 = secretCalculation (num1, num2, num3);
   Answer

   d. num4 = secretCalculation (num1, num2, num3);

Internal Documentation and Subroutines

As you start to create more and more elaborate subroutines, it’s important for you to understand some programming conventions surrounding commenting. While it’s important to comment the lines of code within the subroutine, it is also good practice to provide what is sometimes known as a subroutine header within the program.

A subroutine header is a series of commented lines that explain what the subroutine does. The header also provides information about what parameters are passed to the subroutine, as well as what is returned by the subroutine if it is a method, or whether it is void if nothing is returned.

The following is a good example of a header for the dataOutput procedure:

The following is a good example of a header for the multTwoNums method: