0% Complete
Minds on

MINDS ON

This is the ePortfolio icon. Games Fair Reflection

Play the Four Coin Flip and Five Card Shuffler in the Games Fair. Think about how the probabilities of each outcome might be calculated. These are probabilities that you will learn in later activities, but you are encouraged to start thinking about the complexity of these probabilities. 

GamesFair

Long Description

 
Go To Portfolio
 
Action.

ACTION

Compound Events

In the last activity, you explored the idea of non-mutually exclusive events. These are still mostly single events, they could just be in two categories at the same time. Recall, a student at Eastside Secondary could be in all three classes, but they are still just one student.  

In this activity, we will start to explore multiple events happening, called “compound events.” To help clarify, more than one “action” will be occurring. In this activity, we will explore two actions happening. In the first activity of Unit 2, we will explore more than 2 events happening and keep coming back to the Games Fair games.

Compound Events are events that are created when combining two or more events.  The chance of hitting a target in archery is a compound event. The chance of success depends on the wind.  The outcomes of a 4 coin flip are compound events, they combine all of the outcomes on each of the individual coin. Finding the sum of two dice is a compound event, it combines the number on one die with the number on the other.

This is the example icon. Example 1

Let’s start with the simplest example. Flip two coins.  

  1. What are the total number of ways to flip two coins? Write them all out or organize with a Tree Diagram.
  2. What is the probability that they both come up “tails?”

Solution

  1. Below is a single slide containing multiple steps. Each time you click another step is revealed. To move through all the steps at your own pace, repeatedly click on the slide itself, the right and left arrow icons on the player or the arrow keys on your keyboard. Click the full screen button on the player if you prefer to see a larger version of the steps.

     

  2. P(A) = \frac{1}{4}

 

Over the last couple of activities, we have played with the idea of rolling two dice. Let’s take the opportunity to see all of the outcomes in a different way. 

This is the example icon. Example 2

What are the total number of ways to roll two dice? Write them all out or organize with a Tree Diagram.

Solution

This is a tree diagram with the first section being rolling one die and the second section being rolling a second die. The outcomes combine together to show 36 different sums from 2 to 12.
The different outcomes are combined to make a sum.
 

The Fundamental Counting Principle

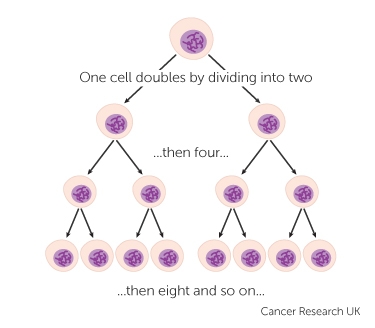
This is an image of one cell dividing into two; then the two cells dividing into 4; then the 4 cells dividing into 8.
Each cell splits to become more cells at each stage, like a tree diagram.
by Cancer Research UK

If you haven’t seen it yet, it may be useful to think of a tree that grows further than 2 levels.  Imagine a bacteria that continues to grow.   What is the operation that helps you determine how many you have after a short amount of time?  

Tree diagrams help to uncover an idea that is essential to probability involving compound events.  

The fundamental counting principle states that if there are m ways to do the first event, n ways to do the second, and so on…  The total number of ways to perform a compound event is m x n.  This is also known as the multiplicative counting principle.  

This is extended to probability by saying that, if A is the first part of a compound event and B is the second, 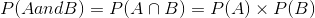 P of A and B equals Probability of A intersect B equals Probability of A times the Probability of B

However, this formula only works when events are independent. A similar one is used for dependent events.

Independent vs. Dependent Events

Independent events are events where the occurrence of one event has no effect on the other event.  

Dependent events are events that have different outcomes depending on what has already happened. The outcome of one event depends on the outcome of another event.  

This is the ePortfolio icon. Games Fair Reflection

Consider the games from the Games Fair.  Are the Four Coin Flip and the Five Card Shuffler independent or dependent?

Go To Portfolio
 

Let’s look at an example of a compound event that uses independent events.

This is the example icon. Example 3

A spinner has 10 different equal-sized sections.  Spin the spinner and draw a card.

This is an image of a wheel with 10 coloured sections.

This is an image of each card in a standard deck of cards on a green background. The suits are in rows with the cards in order from Ace to King.

  1. How many total ways are there to spin the spinner and draw the card?

    Solution

    10 x 52 = 520

 
  1. What is the probability of spinning a 5 and drawing a 5?

    Solution

    A = spinning a 5

    B = drawing a 5.

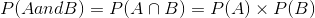
    P of A and B equals Probability of A intersect B equals Probability of A times the Probability of B

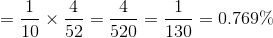
    equals one over 10 time 4 over 520 equals 4 over 520 equals 1 over 130 equals 0.769 percent

    OR  

    A = spinning a 5 and drawing a 5.

    n(A) = 1 x 4 = 4

    n(S) = 10 x 52 = 520  

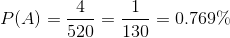
    P of A equals 4 over 520 equals 1 over 130 equals 0.769 percent

 

Note: The solution for 2 was shown in two different ways. Notice that we have some flexibility with what we label A or B. The second solution will come to be known as the slot method using the multiplicative counting principle and will be expanded on in the first activity of Unit 2. The first solution is the probability formula when dealing with two independent events that make up one compound event.

The formula for dependent events is similar, but needs to make note of the fact that the second event depends on the first.   

If A is the first part of a compound event and B is the second which depends on A, then

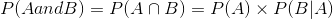P(A and B)=P(A\cap B) = P(A)\times P(B|A)  where P(B|A) 

means “The probability of B given A has already occurred”.

Example: The probability of drawing an ace P(B) given you already drew an ace P(A) is 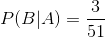P(B|A) =\frac{3}{51}

This is widely known as Conditional Probability.

This is the example icon. Example 4

If the Denver Broncos have an 80% chance of winning at home and a 60% chance of winning on the road (not real stats!), what is the probability that they win any random game in the season, if a random game has a 70% chance of being a home game and 30% chance of being a road game (10 games left in the schedule, 7 at home)?  

This is an image of the field at the Denver Broncos stadium from behind the end-zone. There are fans in the stadium and the game is in progress.

This question actually has two cases which both need to be solved separately then added.  When there are multiple ways to come to a probability, we just add those probabilities together.  Often, we will see the multiple ways as “OR.”  In this example, they win on the road “OR” at home.

Below is a single slide containing multiple steps. Each time you click another step is revealed. To move through all the steps at your own pace, repeatedly click on the slide itself, the right and left arrow icons on the player or the arrow keys on your keyboard. Click the full screen button on the player if you prefer to see a larger version of the steps.

 

Case 1:  Win at Home.  

A = home game

B = Win  

P(A) = 0.7   

P(B|A)=0.8   

P(A and B) = P(A) x P(B|A) = 0.7 x 0.8 = 0.56

Case 2:  Win on Road. 

A = road game  

B = Win  

P(A) = 0.3   

P(B|A)=0.6   

P(A and B) = P(A) x P(B|A) = 0.5 x 0.6 = 0.18

Total probability of winning:  0.56 + 0.18 = 0.74

Therefore, they have a 74% chance of winning any game left in the season.  

 
Consolidation

CONSOLIDATION

This is the dropbox icon. Communication and Thinking

Calculate the probability of three compound events:

  1. made up of Independent events.
  2. made up of Dependent events.
  3. made up of either Independent or Dependent events, but has more than one way to happen (multiple cases).

You must do a tree diagram for one of them. Be sure to state the question and show complete solutions for all three.

Submit Your Work
test text.