0% Complete
Minds on

MINDS ON

This is the ePortfolio icon. Record your thinking

Applying what you learned in the previous unit, describe how you would determine how many ways would there be to have a password for the following lock?  

Note: The lock uses 5 slots and a letter for each slot.

This is an image of old combination roll lock that uses 5 letters. It is sitting on some old paper with caligraphic writing.
Go To Portfolio
Action.

ACTION

Tree Diagrams and the Fundamental Counting Principle

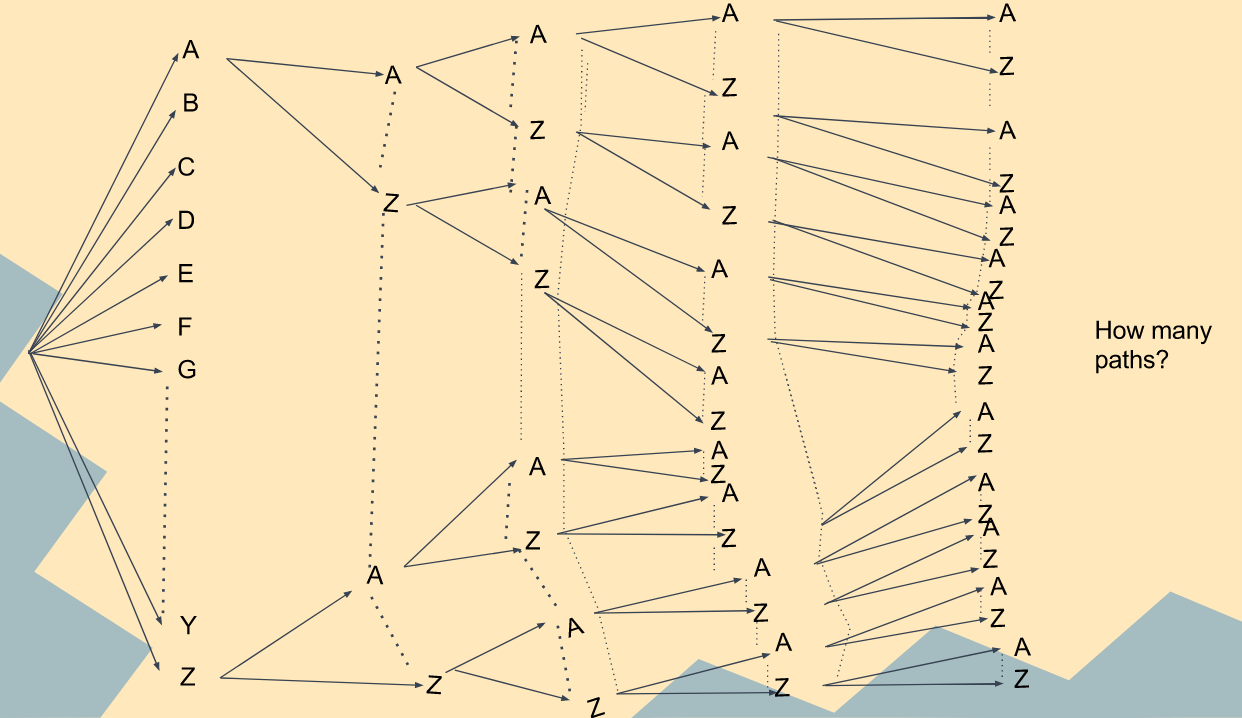
Tree diagrams are great tools to trace the number of outcomes of compound events when they are made up of two independent or dependent events.  

The fundamental counting principle (definition:The fundamental counting principle states that if there are m ways to do the first event, n ways to do the second, and so on…. The total number of ways to perform a compound event it m x n.) is derived from the idea behind tree diagrams and allows you to count the number of outcomes without actually writing them all out.  

The fundamental counting principle states that if there are m ways to do the first event, n ways to do the second, and so on...  The total number of ways to perform a compound event it m x n.

As you can see, a tree diagram is an impractical way when you have something like the lock pictured above.

This is an image of a tree diagram for the lock, a five letter combination.
Even with short-cuts, you can't possibly display all the outcomes.

In the previous unit you also learned the probability formulas for two independent (definition:A compound event where the events that make up the compound event work do not depend on each other.) or dependent (definition:A compound event where the components of the event depend on each other.) events.

The Slot Method

Since it isn’t practical to extend the dependent formula for a compound event that is made up of more than two dependent events, we are going to develop a strategy that uses the fundamental counting principle.  We call it “The Slot Method.”

Using this method, when asked to find a probability of a compound event A, we will find the total number of outcomes, n(S), and the total number of successful outcomes n(A) and use slots for each of the number of events (either independent or dependent) that make up the compound event.  

This is the example icon. Example

Consider the password example.  

  1. How many ways are there to have a password (no restrictions)?
  2. How many ways are there to have a password if you can only use each letter once (no repetition)?
  3. How many ways can the password be written without vowels?

Someone tells you that the password is the word MATCH except in another order.  

  1. How many ways can the password use those letters?
  2. What is the probability that the password starts with M and ends with H?

Solution

Below is a single slide containing multiple steps. Each time you click another step is revealed. To move through all the steps at your own pace, repeatedly click on the slide itself, the right and left arrow icons on the player or the arrow keys on your keyboard. Click the full screen button on the player if you prefer to see a larger version of the steps.

 
 

This is the ePortfolio icon. Slot Method Practice and Reflection

There is a raffle in your class for three prizes.  Names are drawn from a hat and not replaced.  There are 20 people in the class. What is the probability that you and your two best friends win the three prizes?  

Compare your solution to the solution below.  What went well?  What did you miss?  Is there any specific part of the solution that you are having trouble with?

Solution

Below is a single slide containing multiple steps. Each time you click another step is revealed. To move through all the steps at your own pace, repeatedly click on the slide itself, the right and left arrow icons on the player or the arrow keys on your keyboard. Click the full screen button on the player if you prefer to see a larger version of the steps.

 
 
Go To Portfolio
 

Notice that we first write the slots down so that we can ask ourselves:  “How many ways are there to perform this part of the event?” for each of the slots.

Multiple Cases

In the last activity we saw that there may be more than one way that an event can occur (recall Denver Broncos winning at home or on the road).  In that case, we need to calculate the individual probabilities for each of the cases, and add them all together.

This is the ePortfolio icon. Multiple Cases Practice and Reflection

If you rearranged the letters of the word “FACTOR,” what is the probability that the vowels are together? Since there are several ways for the vowels to be together, in different slots throughout the word and with either letter coming first or second, we have to look at each different case separately.  

Try this example before looking at the solution.  

Solution

Below is a single slide containing multiple steps. Each time you click another step is revealed. To move through all the steps at your own pace, repeatedly click on the slide itself, the right and left arrow icons on the player or the arrow keys on your keyboard. Click the full screen button on the player if you prefer to see a larger version of the steps.

 
 
Go To Portfolio
 

The Indirect Method

This is an image of a woman sitting at home with pen and paper thinking while working at a counter with a drink of orange juice.
Probability questions can contain different cases and may take a lot of thought to fully calculate.

This is the example icon. Example

What is the probability that a number password less than 10,000 created from the digits 0,1,2,3,4,5,6,7,8,9, using each digit at most once, contains 6 or 8 or both?

This example has two special elements to it:  

  1. n(S) can be done in multiple ways with a multiple number of slots.  It doesn’t say how many digits could be used.  So, you could have a 1 digit number, 2 digit number, 3 digit number, or a 4 digit number. 
     
  2. n(A) has multiple cases that, when you think about it, get to be complex.  The number could use 6 in any slot, 8 in any slot, or 6 and 8 in any slot.  Not to mention, the question is already complicated enough because it could be a 1,2,3, or 4 digit number.  

For the second point listed above, it is important to start thinking about a different way to count the number of ways.  An indirect way. 

 

This is the ePortfolio icon. Indirect Method Practice and Reflection

What is the probability that a number password less than 10,000 created from the digits 0,1,2,3,4,5,6,7,8,9, using each digit at most once, contains 6 or 8 or both?

Try this question before looking at the solution using the following strategy:

  • Find the total number of ways without the restriction of the 6 or 8 or both.  Note, you still need to consider the cases of 1, 2, 3, or 4 digit numbers.  
  • Also be sure to consider: Is there any digit that can’t occupy any particular spot?
  • Find n(A)'- the complement of A, every element that is not in A

Compare your solution with the solution below.

Solution

Below is a single slide containing multiple steps. Each time you click another step is revealed. To move through all the steps at your own pace, repeatedly click on the slide itself, the right and left arrow icons on the player or the arrow keys on your keyboard. Click the full screen button on the player if you prefer to see a larger version of the steps.

 
 
Go To Portfolio
 
test text.