Distinguishing Patterns by Relationships
Slope and conversions
MINDS ON
You live in a three-dimensional (3D) world in which you constantly interact with objects that have height, width, and depth. When you look at the objects, it is often the two dimensional (2D) aspect of the objects that becomes your focus.
This is similar to the way a photograph captures a three dimensional object onto a two dimensional surface.
You move between the three-dimensional and the two-dimensional views without consciously thinking about it.
You concentrate on the two dimensional view when you need to determine the amount of material required to cover the surface of the object but can also be used when you calculate volume of 3D objects.
 Reflection
Reflection
Look around you. What outlines do you see?
Are they the basic geometrical shapes, like the square, triangle and circle above? Or are they composite shapes, a figure that can be separated into basic shapes?
![ An image displaying three basic shapes (the square, triangle and circle) and showing a composite shape that includes a square with two triangles attached. [Click and drag to move] ](_images/u2a7image20z.jpg)
Write down some of the outlines and the shapes that you see. Save to your Portfolio.
The composite figure in the image above can be divided into three individual shapes - a square, a right triangle and an isosceles triangle. Determine the perimeter (definition:the outside boundary of the figure) and the area (definition:sum of the areas of the individual shapes) of the composite shape.
You can begin by drawing the three shapes and label them with the dimensions given.

Which side length do you need to calculate before you can determine the perimeter? How will you determine the length?
I will need to calculate the hypotenuse of the right triangle using the Pythagorean Theorem.
![ An image of a triangle and calculations shown to show the pythagorean theorem. [Click and drag to move] ](_images/u2a7image22.jpg)
Which are the formulas that you will be using to calculate area?
For the square: A = s2
For the triangles: A = 1/2 bh
Which value do you need to calculate before you can determine the area of each shape? How will you calculate the value?
Most of the values are given but I will need to calculate the height of the isosceles triangle. I can use the Pythagorean Theorem to calculate the height. Since the triangle is isosceles, I know that the height will divide the base into two equal parts of 7.5 cm each.

Determine the perimeter of the composite figure.
Perimeter = sum of the side lengths in the border
P = 15 + 12 + 12 + 23.4 + 18 + 15
P = 95.4 cm

Determine the area of the composite figure.
AnswerArea = sum of individual areas
Area = 225 + 135 + 70.5
Area =430.5 cm2
ACTION
 Mathematical Processes
Mathematical Processes
In this activity, the Mathematical Process Selecting Tools And Computational Strategies is the focus.
Open your document U2 Mathematical Processes and read the descriptions for the process.
As you complete the activity, notice when you are accessing the process and insert your record below the description of the process.
Save to your Portfolio.
The Great Pyramids
Pyramids have been built by civilizations in many parts of the world.The Great Pyramids of Egypt are the ones that often come to mind when the topic arises.

The tallest pyramid in the world is the Great Pyramid of Giza in Egypt. It sits on a square base that has sides measuring 230 m, covering an area of approximately 13 acres. Its height is 137 m and it has four triangular sides rising at an angle of 52 and meeting at the apex (definition:the point at which the triangles meet). The method of construction of the massive structures continues to be debated by historians.
Although different shapes can be used for the base of a pyramid, it is the square based pyramid that continues to be frequently used in architecture throughout the world.


In the process of creating the structures, designers would need to plan the amount of material that will be used for the base and for the four triangular faces. To do this, they will need to know the area of the triangle that makes each of the 4 faces as well as the square that makes the base. You will be learning how to use the side length of the base and the height of the pyramid to calculate these values.
 Word Journal
Word Journal
Open your Word Journal. In the first column, write the word “net.” In the second column write down some everyday meanings for the word. Save to your Portfolio.
The following video takes you through the steps of building a pyramid:
 Building a Pyramid
Building a Pyramid
As you watch how a pyramid can be constructed, make a list of the steps that you observe the person using in the construction.
In your list, include descriptions of the shapes and measurements. You do not need to determine the values on the ruler seen in the video. Instead, notice which lengths are equal and which ones are not.
Use specific vocabulary (definition:vocabulary may include square, triangle, middle, centre, equal, isosceles triangle, height, base, right angle, midpoint, net)
When you have a pattern that you can cut and fold to make a model of a solid shape, the pattern is called a net. Here, the net for a square based pyramid is shown.

You will find the net a useful device to determine the surface area of any three-dimensional shape. Some nets you find online will have tabs along the side edges are not a part of the net; they are a construction addition only. The net above does not have these tabs.
 Word Journal
Word Journal
Return to your Word Journal. Complete the third column for the word “net.” Save to your Portfolio.
From 3D shape to the 2D net
The net for a square based pyramid has 5 sections - 1 square base and 4 congruent (definition:identical in form) triangles - that are joined together to create the pyramid. The triangles connect the base to a point called an apex(definition:the point at which the triangles meet). In previous courses, you have worked with rectangles and triangles, using appropriate formulas to calculate the area of a simple figure or a composite (definition:a figure that consists of two or more geometric shapes) figure. A pyramid is usually described by the side length of the base and the vertical height. This vertical height is not the same as the height that is labelled in the formula for the area of a triangle. What is the relation between the values for the three-dimensional figure and the two-dimensional net? Let’s investigate!
You can use this interactive from geogebra to look at the relationship between the measurements in the pyramid.
Before using the sliders, h ,l and net, look closely at the pyramid.
You should notice that the back side edges are shown in dashed lines.
You should also notice a figure is drawn in dotted lines inside the pyramid.
What is the figure inside the pyramid? How do you know?
There is a right angle triangle. I can see the small square which means 90°. It starts in the centre of the base, rises to the apex, comes down along the triangular face (labelled ℓ) and then follows the base back to centre.
There are three sliders, h, l and net, controlled by the black button on the slider. Also, if you click on the arrow next to the Net button, you can watch the transition from the pyramid to the net and back. Note that you can stop the automatic transition by clicking on the same button, then move the Net button to the right.

You will now have both the pyramid and the net to view at the same time. You should notice that the label on the net, l, is also labelled on the pyramid. The sliders, l and h, will affect the base and height, respectively, labelled on the pyramid.
Begin with the button labelled ‘h’. Move it along the slider.
What changes do you notice as you move the button ‘h’? What stays the same?
The height of the pyramid changes. As the value increases, the height increases and as the value decreases, the height decreases.
In the net, the square base remains the same while the 4 triangular faces get taller and shorter as 'h' increases and decreases. You can also see that as the value of 'h' gets larger, the segment labelled ‘ℓ’ grows as well.
Now experiment with the button labelled ‘l’. Move it along the line.
What changes do you notice as you move the button ‘l’? What stays the same?
The base of the pyramid is changing. As the value increases, the length of the side of the square base increases and as the value decreases, the length of the side decreases. As the side length of the base gets smaller, the triangular face gets steeper. In the net, changing the side length of the base also causes a change in the length of ℓ. As the length of the base increases or decreases, ℓ, increases or decreases, respectively.
When working with right triangles, you know that you can use the the Pythagorean Theorem to determine the length of one side when you know the lengths of the other 2 sides.
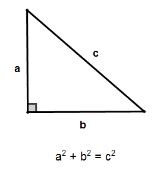
In the interactive, you probably noticed that the right triangle was not labelled using the variables a, b and c; they use h, ℓ and the base of the triangle is not labelled with any variable.

The image shows the right triangle inside the pyramid and then removed from the pyramid. You can see that the height, h, of the pyramid is also the height, h, of the triangle.
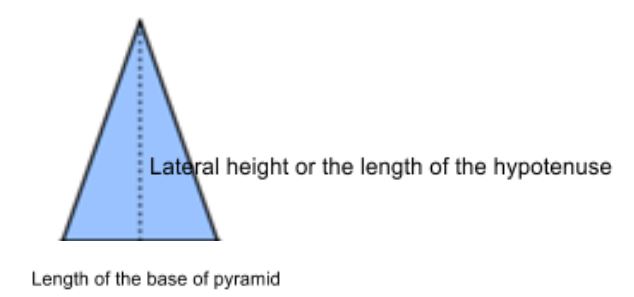
The length along the face of the pyramid, ℓ, is also present in the triangle. In the pyramid, it is the length from the middle of the side of the square to the apex. To distinguish it from the height of the pyramid, it is called the slant height or lateral (definition:referring to the side) height. In the right triangle, it is the side opposite the right angle so it is the hypotenuse.
In the pyramid, the right angle is at the centre of the base. The base of the triangle is 1/2 the length of the base, ℓ, of the pyramid. You can use the variable t to label the right triangle. (t = 1/2 base or t = 1/2 ℓ).
Using the labels from the diagrams, you can see that the Pythagorean Theorem can be written as h2 + t2 = ℓ2, and you can determine the value for the hypotenuse l from the height and base dimensions of the pyramid.
![ An image of a pyramid with a triangular face removed. [Click and drag to move] ](_images/u2a7image55.jpg)
Recap: The hypotenuse is the distance along the triangular face. If the triangular face is “removed” from the drawing of the pyramid then “turned” so you can look directly at the triangular face, you can see a 2D triangle. The height for the 2D triangle is the hypotenuse of the right triangle inside the pyramid.
Take a look the revolving pyramid here and separate it into its 5 surfaces. You can see the change from a three dimensional object to 5 two dimensional shapes.
When you have the value for the hypotenuse, you can use the formula for the area of a triangle to calculate the surface area of one lateral face, which is a face in the pyramid that is not the base.
With the area for one lateral face, you now have all the information to calculate the surface area of the pyramid.
![ An image showing how the surface area of a pyramid can be calculated by determing the surface area of the base and the surface area of the four lateral faces. [Click and drag to move] ](_images/u2a7image7.jpg)
Calculating the Surface Area of the Great Pyramid
The following interactive will help you develop and understanding of the steps involved in calculating the surface area of the Great Pyramid.
greatPyramid
Calculating the Surface Area of a given pyramid
The following interactive will help you develop and understanding of the steps involved in calculating the surface area of another pyramid.
sideIs30
Did you know that in Canada, abbreviations for imperial weights and measures use the same form for singular and plural? Area is expressed using the abbreviation sq. along with the unit abbreviation rather than using the superscript 2 with the unit abbreviation. For example, sq. in. instead of in2.
Conversion between Metric and Imperial Systems
You probably noticed that one surface area problem used metric units and the other used imperial units. In Unit 1, you investigated the relationship between the metric unit, centimetres, and the imperial unit, inches. You created a graph and found an equation using the online graphing tool.
Earlier in this unit, you were learning to determine the slope and y-intercept of a linear relation. You will use your new skills as you revisit the topic of unit conversion, scale factors and slope.
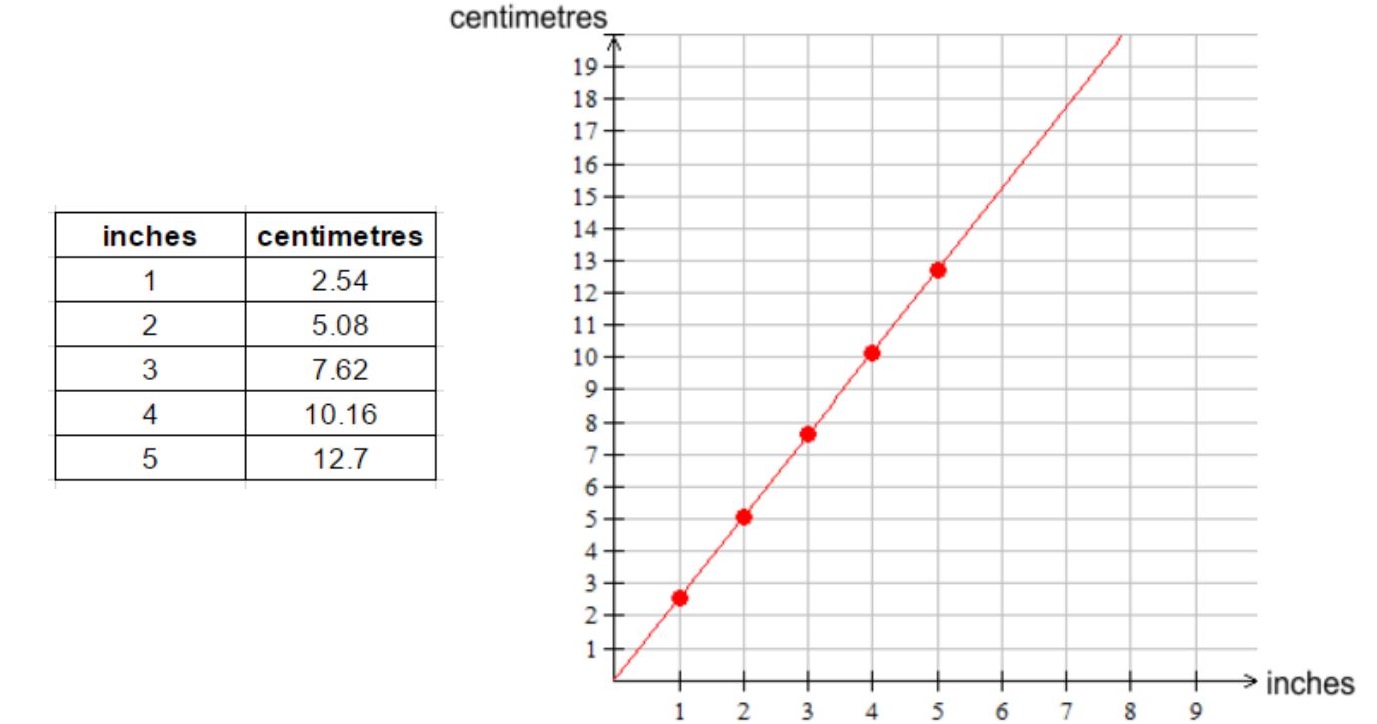
Your table of values and graph from the investigation in Unit 1 would be similar to these. You can use the values in the table of values or the graph to determine the equation of the line.
So how could you determine the equation of the line for the relation between centimeters and inches?
You can choose any two points from the table. This will be more accurate than reading the values from the graph.If you chose the two points (1, 2.54) and (4, 1016) your slope calculation would look like this. You can use this as a model for your own slope calculation.
Calculate the Slope
Calculate the y-intercept
Equation of the line is y = 2.54x. The graph passes through the origin.
Think carefully about the calculations done above, to determine the equation of the line for the relation between centimeters and inches.
What is x in the equation?
What does y represent in the equation?
What does the equation tell you?
What variables would you choose to replace x and y to represent the quantities in this specific problem?
How can you use the equation to convert between metric units and imperial units? Can this equation be used for any metric/imperial measurement conversions or just certain conversions? (e.g.: Could you use this equation to convert metres to inches?)
Using the Equation of a Line
Now let's use the equation to determine the number of centimetres that are equivalent to 2 ¾ inches.
To use the equation, you need to rewrite the inches in decimal notation so 2 ¾ = 2.75 inches.
y = 2.54x and x = 2.75
y = 2.54 (2.75)
y = 6.98 cm
So, 2 ¾ inches is equivalent to 6.98 cm.
Now let's use the equation to determine the number of inches that are equivalent to 13.34 cm.
You have the value for y and will solve for x.
y = 2.54x and y = 13.34
13.34 = 2.54x
13.34/2.54 = 2.54x/2.54
5.25 = x
So 13.34 centimetres is equivalent to 5.25 inches.
Rewriting the Equation
You have seen that you can use the same equation to convert from inches to centimetres or from centimetres to inches. For the conversion from inches to centimetres, you multiply by 2.54 and for the conversion from centimetres to inches, you divide by 2.54.
If you rewrite the equation using variables related to the topic, you can see this more clearly.
If you let ‘c’ represent the number of centimetres and ‘i’ represent the number of inches.
The equation y = 2.54x becomes c = 2.54i.
We can rearrange the equation to solve for i:
The independent variable is length in centimetres and the dependent variable is length in inches.
Using x and y as the variables, the equation becomes y = 1/2.54 or y = 0.39x.
Drawing the graph of the relation that converts centimetres to inches
What happens when we draw the graph of the relation that converts centimeters to inches and then we compare it with the graph that converts inches to centimeters. What will be the same? What will be different? Let's see...
Both graphs are linear relations that pass through the origin; that means that the x-intercept and the y-intercept are both 0. The labels on the two graphs are interchanged. The graph that converts centimetres to inches has a line that is not as steep as the line that converts inches to centimetres. Linear relations that pass through the origin are often called a direct variation.
Think about what this relation is about. Why would you expect the graph of this relation to go through the origin? (You could have guessed this before doing any data gathering. Why?)
In the Units activity in Unit 1, you identified the scale factor or the conversion factor in the equation. You can see that this factor is also the slope of a linear relation that passes through the origin. When you discuss a conversion factor, the units are attached. Here, you found the conversion factor for converting inches to centimetres; it is 2.54 cm/in (this is read as 2.54 centimetres per inch). You also found the conversion factor for inches to centimetres; it ia 1/2.54 or 0.39 in/cm (this is read as 1 inch per 2.54 centimetres or .39 in per centimetre).
You could also find the conversion factor or the slope of the linear relations between other sets of units e.g. metres and yards, miles and kilometres.
Conversion factors and relation equations will convert a length in one unit to a length in another. You could use the conversion tools to change the units before you started all the calculations. But what do you do if you realize that the total surface area needs to be given in imperial units after you have completed all your calculations?
Do you think that the relationship between square inches and centimetres squared will also be linear? What might the conversion factor be?
Investigating Conversions for Square Units (Area)
Download and open U2A7 Converting Area.
- Complete the area calculations for the squares in both inches and centimetres.
- Use the values to create the table of values with sq. in as the independent variable and cm2 as the dependent variable.
- Using the ordered pairs in the table, create a graph.
- What does the graph tell you? Is the relation linear or non-linear? Is that what you expected?
- Determine the equation that could be used to convert area from square inches to centimetres squared.
Why does it make sense that the relation that models conversion of square inches to centimetres squared is still linear? Isn’t area a quadratic model?
Now consider the relation between area measured in square inches and area measured in centimetres squared.
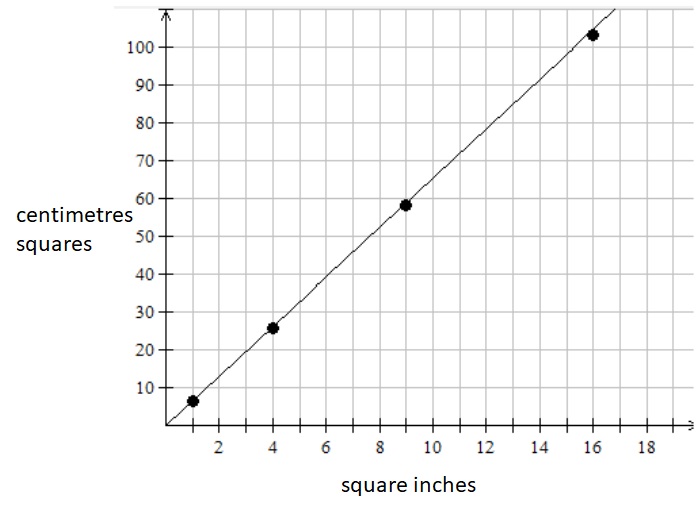
It is a linear relation . The graph is a straight line and passes through the origin so both intercepts are 0. The equation for the relation is y = 6.54x where x is the area measurement in square inches and y is the measurement in centimetres squared.

This means that every square inch is equivalent to 6.45 square centimetres. A square inch covers more area than a square centimetre.
Now how can we use the equation to convert an area given in square inches to an area in centimetres squared?
We can substitute the area value for x and multiply. The slope value, 6.45, is the conversion factor, 6.45 cm2/sq. in.
Now how can you use the equation to convert an area in cm2 to an area sq. in?
We can substitute the area value for y and divide by 6.54.
An equation can be determined to convert cm2 to sq. in as you did to change centimetres to inches. Again, you can rewrite the equation using variables related to the topic to see this more clearly.
If you let ‘C’ represent the number of centimetres squared and ‘I’ represent the number of square inches.
The equation y = 6.45x
becomes C = 6.45I
We can rearrange the equation to solve for I:
When you work with conversion factors, there is often the possibility for incorrect answers. In most cases, the conversion factor is the best value to use to convert one measurement to another. In general, calculations should be carried through using the given measurements. Using this value and a reliable conversion factor should create a value in the new measurement system. When you use a conversion factor that has been rounded, be aware that your calculated value will not be exact.
Earlier in the activity you read about the Great Pyramids and calculated the surface area of the largest pyramid in the world. Modern day architecture continues to use pyramids in creating dramatic buildings in different locations with different purposes in their final use.
Practice Question
The Walter Pyramid in Long Beach California is an athletic facility at their local state college.
The Walter Pyramid has a square base with a side length of 345 ft. and a height of 191 ft.
Determine the difference in the surface area of the Great Pyramid and the Walter Pyramid.
You can review your work and check your answer by viewing this video:
CONSOLIDATION
You learned to use a conversion factor to change inches to centimetres and centimetres to inches. You were also able to make conversions between imperial and metric measures of area. You noticed that the conversion factors were the same value as the slope of linear relation between the two units and that the linear relation is a direct variation or a relation where the x - intercept and y-intercept are both zero. Conversion of units can be made between the imperial system and the metric system (e.g. inches to centimetres). It is also possible to make conversions between different units within each system (e.g. centimetres to metres or square feet to square yards).
Use the online converter to determine some other conversion factors and their accompanying linear equations.
To use the conversion table.
- Type in the starting unit and you will notice a choice of options.
- Move to the the row that has the ending unit and click Table.
- Select the Table Options; the table will change with each option change
- Set increments to 1
- Set accuracy to 3 significant figures
- Set format to Decimal
- Look at the row for 1 starting unit - what is the value for the ending unit?
- Look at the row for 2 starting units - is the value double of the preceding value?
- Record the conversion factor.
Along with determining the conversion factors, there are questions where you are asked to use a conversion factors.
1. Determine the conversion factor for metres (metric) to yards (imperial). How many dimensions does this factor involve? How do you know that the graph of yards versus metres would pass through (0, 0)? Write the equation for the relation.
The unit involves one dimension because we can measure it with a device. As the number of metres (m) increases by 1, the number of yards (yd) increases by 1.09. So the conversion factor is 1.09 yd./m.
The graph would pass through the origin (0, 0) because for 0 metres there are 0 yards.
The equation is y = 1.09x.
2. Determine the conversion factor for cups (imperial) to millilitres (metric) - choose Canadian cups. How many dimensions does this factor involve? How do you know that the graph of cups versus millilitres would pass through (0, 0)? Write the equation for the relation.
There are three dimensions - height, width and depth are within this measurement. As the number of cups (c) increases by 1, the number of millilitres (mL) increases by 227.30. So the conversion factor is 227.3 mL/c.
The graph would pass through the origin (0, 0) because for 0 cups there are 0 millilitres.
The equation is y = 227.3x.
3. Determine the conversion factor for square feet (imperial) to square yards (imperial). How many dimensions does this factor involve? How do you know that the graph of square feet versus square yards would pass through (0, 0)? Write the equation for the relation.
There are two dimensions involved in the factor - length and width or length and depth. As the number of square feet (sq. ft) increases by 1, the number of square yards (sq. yd) increases by 0.111. The conversion factor is 0.111 sq. yd/sq. ft.
The graph would pass through the origin because for 0 sq. ft there are 0 sq. yd.
The equation is y = 0.111x.
4. Determine the conversion factor for cubic metres (metric) to cubic centimetres (metric). How many dimensions does this factor involve? How do you know that the graph of cubic metres versus cubic centimetres would pass through (0, 0)? Write the equation for the relation.
As the number of cubic metres (m3sup>) increases by 1, the number of cubic centimetres (cm3) increases by 1 000 000. The conversion factor is 1 000 000 cm3/m3. The graph passes through the origin because for 0 m3 there are 0 cm3.
The equation is y = 1 000 000x.
 Mathematical Processes
Mathematical Processes
In this activity, the Mathematical Process Selecting Tools And Computational Strategies is the focus.
Open your document U2 Mathematical Processes and complete your record of when you used the process of Selecting Tools and Computational Strategies.
Save to your Portfolio.
 Reflection
Reflection
Open your Reflection Journal U2 Reflections. Think about the new ideas, vocabulary, and skills that you learned in this activity. How do they connect to the previous information that you know from other courses? What other connections did you make during the activity? Review the rubric for the Journal. Choose two sentence stems to lead your reflection following this activity.
Congratulations, you have completed Unit 2, Activity 7. You may move on to Unit 2, Activity 8.