0% Complete
Minds on

MINDS ON

Triangles in a Puzzle

A tangram is a Chinese geometric puzzle. It is a square that is cut into seven pieces - 5 triangles, a square and a parallelogram. 

An image of a tangram with seven shapes placed ina way that creates a square.

 

The shapes can be arranged to create various other shapes.

the shapes of a tangram arranged as a house, a bird and a sailboat.

 

Tangrams are available in many sizes and colours. Regardless of the size or colour, the relation between the shapes remains the same. You will investigate the relation between the 5 triangles in the puzzle. Print and cut out the 7 puzzle pieces (tans) in the tangram U2A8 Tangram.

An image showing the six different triangles that include a write angle triangle, an obtuse triangle, an acute triangle, an equilateral triangle, an isoceles triangle and a scalene triangle.

 

Triangles can be classified using the measure of the angles (acute, obtuse or right angle) in the triangle as well as using the number of equal sides (equilateral, isosceles, scalene) in the triangle.

What kinds of triangles can you find in the tangram? Describe them using correct vocabulary.

Answer

There are 5 right isosceles triangles. Each triangle has a right angle and the two legs of each triangle are the same length. There are 2 large, 1 medium and 2 small triangles.

 

If the triangles are right isosceles triangles, what is the angle measure for the non-right angles?

Answer

Each non-right angle measures 45°.
Open Right Isosceles Triangles to check this out.

 

This tells me that the 5 triangles are:
a) Equal
b) Equivalent
c) Similar
d) Symmetrical

Answer

c. Similar. The term that describes triangles that have the same shape (i,e, the same sized angles) but do not necessarily have the same side lengths is similar.

 

You also know that the ratio of corresponding sides of two similar triangles is equal. When you write the two ratios as an equation, it is called a proportion(definition:statement that two ratios are equal).

An image of the equation that shows hypotenuse of triangle 1 divided by hypotenuse of triangle 2 equals length of side in triangle 1 divided by length of side in triangle 2.

 

You can use the proportion to determine an unknown side length, if you know the other 3, by substituting the known lengths and solving for the unknown length.   

You probably notice that some edges of the triangles follow the grid lines while others cross through the grid lines.

You can count the number of units along the hypotenuse of the smallest triangle (10 units) as well as the number of units along the hypotenuse of the largest triangle (20 units).

Because the triangles are similar, you know that all the side lengths of the largest triangle are two times the side lengths of the smallest triangle. The length of the legs in either triangle are not known since you can not count the number of units.

Why would it be incorrect to count the squares to measure the length of the leg of the smallest triangle?

Answer

The leg runs diagonally through the square and we don’t know the length of the diagonal, so we can’t count.

 

What mathematical relation connects the side lengths in a right triangle?

Answer

The Pythagorean Theorem states the relationship between the legs and the hypotenuse in a right triangle.

 

You have usually used the Pythagorean Theorem for a right triangle that has three different side lengths. In this example, you will see how the Pythagorean Theorem can be used to determine the length of the legs in a right isoceles triangle (a triangle that has two sides of equal length is isosceles).

1. Information: hypotenuse =10 units, a and b are equal so a = b.

An image of a write isoceles triangle.

 

2. Write the formula, using the chosen variables. Since a = b, you can use the same variable to represent both. Choose a, for example.

a2 + a2 = c2

 

An image of a write isosceles triangle with squares drawn as part of each side.

 

3. Substitute the known values for the variables into the equation. Simplify if possible: Since a2 and a2 are like terms (same variable raised to the same power), they can be added together.

a2 + a2 = 102
2a2 = 102
An image of a write angle triangle with squares drawn attached to each side. The two smaller squares are labeled as a squared and the larger square is labeled as 10 squared.

 

4. Calculate. Square 10. Divide both sides by 2. Take the square root of each side.

An equation that shows 2 a squared equals 10 squared. 2 a squared therefore equals 100. Divide both sides by two giving a squared equals 50. Take the square root of both sides to give 7.07106.

 

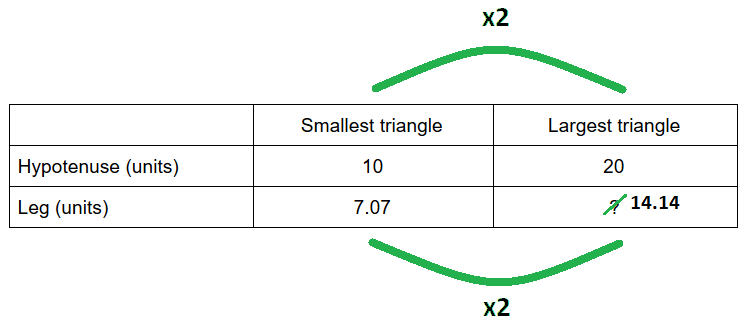
After rounding to two decimal places, we can confirm that the length of the leg in the smallest triangle is therefore 7.07 units.

Determining Unknown Length in Largest Triangle

Now that you have the length of the leg in the small triangle, you can use the proportion (definition:statement that two ratios are equal) to determine the length of the leg in the largest triangle.

There are different ways that you can use to solve a proportion. You can use an equation, a ratio table or a graph.

Method #1 - Solving the proportion as an equation:

1. Information: hypotenuse large = 2, hypotenuse small = 10, leg (length of side) in large = ?, leg (length of side) in small = 7.07.

An equation that shows the hypotenuse of large triangle divided by the hypotnuse of the small triangle equals the length of side in large triangle divided by the length of side in small triangle.


2. Substitute the values into the formula. Notice that there are now values in 3 of the 4 positions.

An image of the equation 2o divided by 10 equals an unknown divided by 7.07.


3. One way to solve for the unknown value, ?,  is to simplify the left side of the equation.

An image of the equation two equals an unkown divided by 7.07.


4. You can multiply both sides of the equation by 7.07 to simplify the right side.

An image of the equation two times 7.07 equals an unknown divided by 7.07 multiplied by 7.07.


5. Simplify both sides of the equation.

14.14 = ?


The length of the leg is 14.14 units, twice the length of the leg of the smallest triangle.
 

Method # 2 - Using a Ratio Table:

A ratio table is a table where equivalent ratios or rates fill the columns. We can fill the first column with the values for the smallest triangle and the second column with the values for the largest triangle.

An image of a table that indicates that the hypotenuse and leg of the smallest triangle are 10 and 7.07 respectively. The hypotenuse and leg of the largest triangle are 20 and unknown respectively. Since the hypotenuse was multiplied by 2, we can multiply the leg to find that the leg value of the largest triangle is 14.14.


Method # 3 - Using a Linear Relation

You have seen previously that proportional relations pass through the origin. You can create a graph and an equation using the values for the hypotenuse and the leg of the smallest triangle (10, 7.07) and the origin (0, 0).

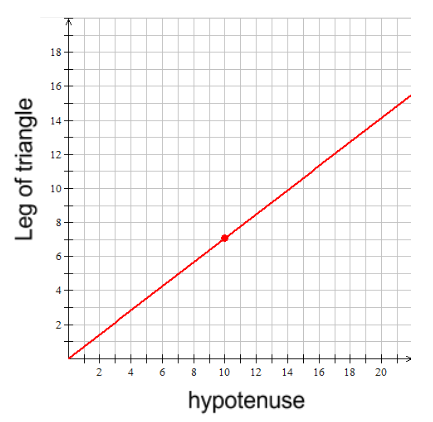
An image of a grid with hypotenuse on the x axis and leg of triangle on the y axis. The line on the grid passes travels from (0,0) to (20,14).


To determine the equation of the line, you can calculate the slope of the line.

An image with the equation m equals rise over run which equals change in y divided by change in x. m equals 7.07 - 0 divided by 10 minus 0. m equals 7.07 dived by 10.

 

From these calculations we find that m = 0.71 when rounded to 2 decimal places.

Since the y-intercept is 0 the equation for the line is y = 0.71x.

An image of a grid with hypotenuse on the x axis and leg of triangle on the y axis. The line on the grid passes travels from (0,0) to (20,14). Point (20, 14) is highlighted.


You can estimate the point from the graph (when x = 20) or substitute the value x = 20 into the equation to get a more accurate answer.

y = 0.71x

y = 0.71(20)

y  = 14.14

An image of the two write angle triangles. The small triangle is labeled with side lengths of 10, 7.07 and 7.07. The large triangle is labeled with side lengths of 20, 14.14 and 14.14.


You have all the side lengths in the smallest and largest triangles.

Determining the Length of the Hypotenuse in the Middle Triangle

You can use the grid lines to determine the length of a leg in the middle triangle.

Method #1 - Solving the proportion as an equation

1. Information: hypotenuse medium = ?, hypotenuse small = 10, leg in medium = 10, leg in small = 7.07

An image showing the equation hypotenuse of medium triangle divided by hypotenuse of small triangle equals the length of the side of the medium triangle divided by the length of the side in the small triangle.


2. Substitute the values into the formula. Notice that there are now values in 3 of the 4 positions.

An image showing the equation unknown divided by 10 equals 10 divided by 7.07.


3. One way to solve for the unknown value of ? is to simplify the equation.

An image showing the equation unknown divided by 10 equals 1.414.


4. You can multiply both sides of the equation by 10 to simplify the equation.

An image showing the equation unknown divided by 10 multiplied by 10 equals 1.414 multiplied by 10.

5. Simplify both sides of the equation.

? = 14.14


From these calculations we find that the length of the hypotenuse is 14.14 units.

Method # 2 - Using a Ratio Table

The value to use for multiplication is not as easily seen. We can start by determining the unit rate (an amount for one item) for the leg.

An image of a table showing that the hypotenuse and leg of the smallest triangle are equal to 10 and 7.07 respectively. The values of the hypotenuse and leg of a middle triangle are unknown and 10 respectively. We can add a middle coumn and divide the hypotenuse and leg by 7.07. We can then multiply these values by 10 to find the value of the hypotenuse of the middle triangle is 14.14.

 

We can tell by the work in the table that the of the hypotenuse on the middle triangle is 14.14 units.

Method # 3 - Using a Linear Relation

Since the middle triangle is similar to the other two triangles, the same graph and equation can be used. With this problem, you have the leg of the triangle which is the dependent value (y) in the representation.

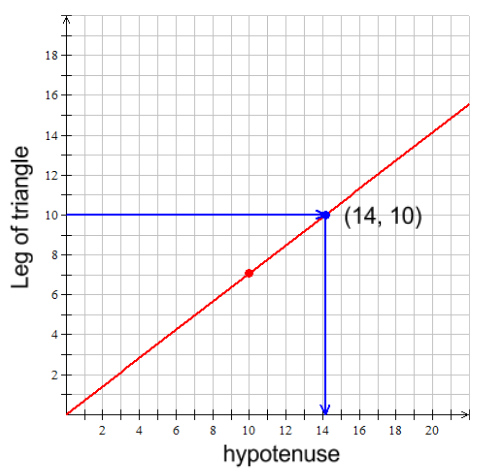
An image of a graph with hypotenuse on the x axis and leg of triangle on the y axis. The point (14, 10) is highlighted.


Using the graph, you can approximate the value for x as 14. You can also use the equation.

y  = 0.71x

You know the value for y is 10.

Substitute y = 10 into the equation.

10 = 0.71x

10/7.1  = x

14.14 = x

The hypotenuse is 14.14 units.

Method #4 - Using the Pythagorean Theorem

Since you know the 2 leg lengths for the triangle and need to determine the hypotenuse, you can use the Pythagorean Theorem to determine the hypotenuse.

An image showing a triangle with two equals side lengths of 10. The final side length is unknown.
An image of the equation a squared plus b squared equals c squared. We can add values to get ten squared plus ten squared equals c squared. This gives us 100 times 100 equals c squared or 200 equals c squared. If we take the square root of both sides we find that c equals 14.14.


The hypotenuse is 14.14 units.

There are often different methods for finding a solution. It is useful to know how to use different solution methods. One method may sometimes be a simpler method to use than others.

The following video will take you through some further practice solving proportions:

 
Action.

ACTION

This is the Portfolio icon. Mathematical Processes

In this activity, the Mathematical Process Connecting is the focus.

Open your document U2 Mathematical Processes and read the descriptions for the process.

As you complete the activity, notice when you are making connections and insert your record below the description of the process.

Go To Portfolio
 

Slope and Scale Factor

An image of two similar triangles. The larger triangle has side lengths of 10.4 cm, 13.0 cm and 6.9 cm and angles of 95, 32 and 53 degrees. The smaller triangle has side lengths of 7.7 cm, 9.6 cm and 5.1 cm and angles of 95, 32 and 53 degrees.


Δ ABC and Δ DEF are similar triangles.

You know this because each triangle has angles of 95(deg), 32(deg) and 53(deg). You can calculate the ratio of the corresponding sides to determine the scale factor between the two triangles.

An image of table showing values showing side length of AB over DE has a ratio of 5.1 over 6.9 and a scale factor of 0.74. Side lengths BC over EF have a ratio of 7.7 over 10.4 and a scale factor of 0.74. Side lengths AC over DF have a ratio of 9.6 over 13 and a ratio of 0.74.


The scale factor is a value between 0 and 1 so you know that Δ ABC is a smaller triangle Δ DEF. Each side length is reduced by a factor of 0.74, or is 74% shorter than its corresponding side in Δ DEF.

An image of a graph with triangle MNP on the x axis and triangle FGH on the y axis. We can calculate slope to find that it equals 1.4.


You also know that proportional relations are linear relations that pass through the origin. You can create a graph of the corresponding lengths.

If the side lengths of Δ DEF are used for the independent values and the side lengths of Δ ABC are used for the dependent values, the ordered pairs on the graph are (6.9, 5.1), (10.4, 7.7) and (13, 9.6). You can also add (0, 0) to the graph. (You should be able to explain why).

Watch the short video that shows graphing the ordered pairs and determining the equation of the line that passes through the points.

 

You can also calculate the slope and determine the equation of the line using the formulas. View the short video to see the calculations.

 

In many situations, you do not know the values of all the side lengths of a set of two similar triangles. If the triangles are similar and you know one set of corresponding sides, you can use the side lengths as an ordered pair, along with (0, 0), to create a graph. As you sketch your graph, you are defining the independent (side lengths in triangle 1) and dependent (side lengths in triangle 2) variables for the equation of the line. When you determine the slope to write the equation, you are also determining the scale factor relating the two similar triangles.

The slope of a linear relation, or the scale factor between two similar triangles is the same value and can be used to determine a side length in similar triangles. Which way works better for you? Do you prefer to reason proportionally with ratios or do you prefer to use the equation of the proportional relationship? As you read through the following examples, look at the differences and see if you prefer one way more than the other.

Let’s take a look at an example.

Example 1

Δ MNP  ~ Δ FGH

Statement above includes the ~ symbol, which is used to replace the words “is similar to”.

So the statement above would read: triangle MNP is similar to triangle FGH.

Determine the measure of (ang) H and the length of NM.

Solution:

To determine ∠H:

The sum of the angles in a triangle is: 180°; so ∠F + ∠G + ∠H = 180°.

Using the values in the diagram:

108° + 32° + ∠H = 180°

140° + ∠H = 180°

 ∠H = 180° - 140°

 ∠H = 40°

You have verified that ∠H is 40°. Since you were told the triangles are similar, you could have used the value directly from Δ MNP.

​ An image with two similar triangles. The smaller triangle is labeled MNP and has side lengths of 11.7 cm, 6.5 cm and an angle of 40 degrees. The larger triangle is labeled FGH and has a side length of 16.4 cm and two angles of 32 and 108 degrees. [Click and drag to move] ​

 

You are given the side length of side GH in ΔFGH. What other side lengths could you determine given the information in the image?
a) none
b) FG only
c) FH only
d) FG and FH

Answer

b) FG only. It is not possible to find the length of FH since you do not know the length of the corresponding side, MP, in ΔMNP.

Now let's determine the length of FG.

Use a Proportion:

Δ FGH is larger than Δ MNP so the scale factor for the enlargement will be a value greater than 1.

Determine the ratio of the corresponding sides:

An image showing the calculation GH over NP equals 16.4 over 11.7 which equald 1.4.


So the ratio for GH:NP is... 1.4 : 1

An image of calculations showing GH over NP equals FG over NM which equals 1.4. This can be simplified to FG over 6.5 equals 1.4. We can multiply both side by 6.5 to get FG equals 9.1 cm.

Use an Equation:

​ An image of a graph with triangle MNP on the x axis and triangle FGH on the y axis. The slope of the line on the graph is calculated to equal 1.4. [Click and drag to move] ​


If (0, 0) and (11.7, 16.4) are plotted, then 1.4 is also the slope of the line of the proportional relationship. The equation will be y = 1.4x where x is the side length on Δ MNP and y is the side length on Δ FGH.

To calculate FG (y), using the equation, with x = NM = 6.5

y = 1.4x

FG = 1.4(6.5)

FG = 9.1 cm

Example 2

An image of two triangles joing together at their corners. Triangle one is labeled FGJ with side lengths of 11.2 cm and 8.4 cm and angles of 98 degrees and 34 degrees. Triangle two is labeled HIJ and has two sides of 4.9 cm and 8.6 cm and an angle of 98 degrees.


In the picture, Δ FGJ ~ Δ IHJ. Determine the measure of all the unknown angles and the unknown side lengths in the two triangles.

To determine ∠F, ∠I and ∠HJI:

The sum of the angles in a triangle is: 180°; so ∠F + ∠G + ∠J = 180°.

Using the values in the diagram:

 ∠F + 98° + 34° = 180°

∠F + 132° = 180°

∠F = 180° - 132°

∠F = 48°

In Δ IHJ, you probably notice that  ∠HJI and ∠FJG are opposite each other. You may remember from previous courses that the angles formed by two intersecting lines are always equal. So ∠HJI = 34°. And ∠I corresponds to ∠F so ∠I = 48°.

You may find it useful to redraw one triangle and orient it so that the corresponding sides are more easily viewed. Δ IHJ has been rotated to align the corresponding angles.  

An image of two triangles joing together at their corners. Triangle one is labeled FGJ with side lengths of 11.2 cm and 8.4 cm and angles of 98 degrees and 34 degrees. Triangle two is labeled HIJ and has two sides of 4.9 cm and 8.6 cm and an angle of 98 degrees. Triangle HIJ has been extrapolated from the diagram and includes two extra angle values of 48 degrees and 34 degrees.


Now let's determine the lengths of FG and HJ.

Use a Proportion:

To determine the unknown lengths you can use the corresponding sides FJ and IJ to determine a ratio between the two triangles. Set up the ratio of Δ FGJ : Δ HIJ.

An image of an equation showing FJ over IJ equals 11.2 over 8.6 which equals 1.3.

So this tells use that scale factor is 1.3.

Now let's solve for FG:

An image of the calculations involved in solving for FG. FG over HI equals 1.3 therefore FG over 4.9 equals 1.3. We can multiply both sides by 4.9 to find that FG equals 6.4 cm.


The value 6.4 seems reasonable, the length needs to be greater than the length in the smaller triangle.

Now let's solve for HJ:

An image showing the calculations involved in solving for HJ. GJ over HJ equals 1.3. We can replace GJ with 8.4 so that 8.4 over HJ equals 1.3. We can multiply both side by HJ to get 8.4 equals 1.3 times HJ. We can divide both sides by 1.3 to find that HJ equals 6.4.


The value 6.4 seems reasonable, the length needs to be less than the length in the larger triangle.

Use an Equation

An image of a grid with triangle FGJ on the x axis and triangle HIJ on the y axis. A calculation is included that determines that the slope of the line on grid is equal to 1.3.


When you use the lengths of the corresponding sides and write the ordered pair (8.6, 11.2), you are using the side lengths of the smaller triangle, Δ HIJ, as the independent variable (x) and the side lengths of the larger triangle, Δ FGJ , as the dependent variable (y).

An image of two triangles joing together at their corners. Triangle one is labeled FGJ with side lengths of 11.2 cm and 8.4 cm and angles of 98 degrees and 34 degrees. Triangle two is labeled HIJ and has two sides of 4.9 cm and 8.6 cm and an angle of 98 degrees.


The slope is calculated and is the same as the scale factor. 

The equation of the line is y = 1.3x

To determine the length FG in Δ FGJ, the larger triangle, you use the length of HI in the equation.

HI = 4.9 and is substituted for the value of x.

y = 1.3x

y = 1.3 (4.9)

y = 6.4 cm

The value 6.4 seems reasonable, the length needs to be larger than the length in the smaller triangle.

To determine the length HJ in Δ HIJ, the smaller triangle, you use the length of GJ in the equation.

GJ = 8.4 and is substituted for the value of y.

y = 1.3x

8.4 = 1.3x

8.4/1.3 = x

x = 6.5 cm

The value 6.5 seems reasonable, the length needs to be less than the length in the larger triangle.

An image of both triangles again. This time the unknown side of FG is labeled as 6.4 cm. The unknown side HI is labeled as 4.9 cm.


You can label the initial diagram with the calculated values and check to see if the calculated values are reasonable:

  • HI corresponds to FG and both have the shortest lengths in the triangles;
  • IJ corresponds with FJ and both have the longest lengths in the triangles;
  • HJ corresponds with GJ and have the middle lengths in the triangles.

Example 3

Determine the height of the flagpole by using the length of its shadow on the ground.

An image of a Canadian flag hanging from a flag pole.


When you look at the shadow created by two different objects, the triangles formed between the shadow on the ground, the object and the sun’s rays will be similar triangles if both objects are at right angles to the ground. The sun is far enough away from the earth that the rays of light are understood as being parallel. This means that the acute angles at the ground will be equal and the acute angles at the peak of the object will be equal.

To do this, you need to use an object that has a known height (or length) and measure the length of the shadow of the known object. Here, we will use a metre stick held at a 90 degree angle to the ground as our object.

An image of a flag pole with a shadow length of 8.5 m. Next to it is a metre stick with a shadow length of 0.63 cm.

 

You may find it easier to see the similar triangles if the third side is drawn in.

​An image of a flag pole with a shadow length of 8.5 m. Next to it is a metre stick with a shadow length of 0.63 cm. This time the rays of light are drawn to create a triangle with both figures. [Click and drag to move] ​


You can create the graph of the proportional relationship using the information you know about the metre stick to create one ordered pair (0.63, 1.00), (shadow length, actual length), and (0, 0) as the second ordered pair, to calculate the slope of the line.

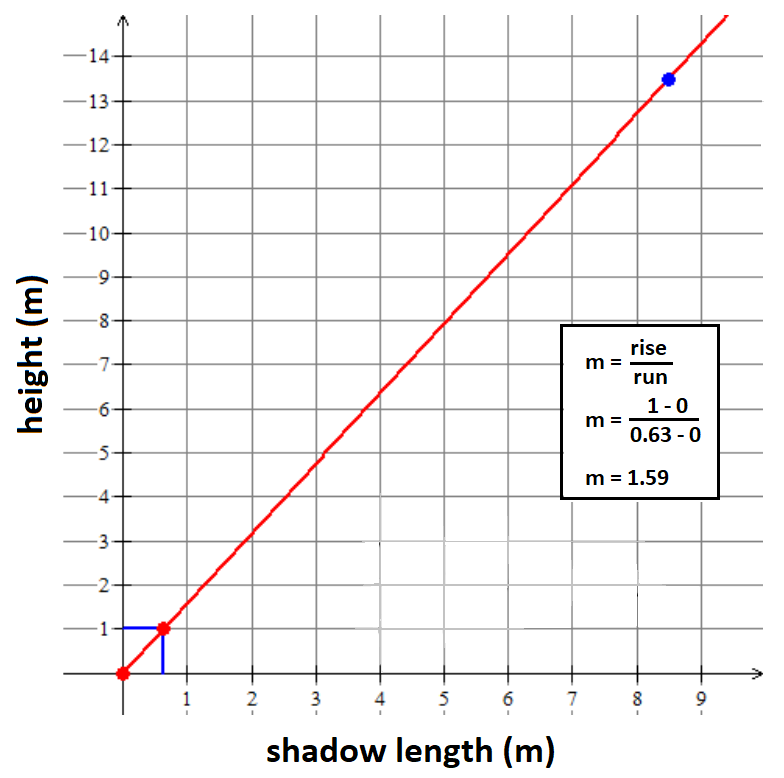
An image of a grid with shadow length on the x axis and height on the y axis. the slope is calculated on the graph equals 1.59.


The equation that represents the relationship is y = 1.6x (we will round to 1 decimal place).

To determine the actual height of the flagpole, substitute x = 8.5 m into the equation and solve for y.

y = 1.6x

y = 1.6 (8.5)

y = 14 m

The height of the flagpole is 14 m.

Review

An image of two triangles. Triangle ABC has two angles labeled 56 degrees and 30 degrees. Triangle DEF has two angles labeled 30 degrees and 56 degrees.


Given the two triangles, ΔABC and ΔDEF, which of the following statements is true?

a. AB corresponds to DF
b. AB corresponds to DE
c. AC corresponds to EF
d. BC corresponds to DE

Answer

b) AB corresponds to DE

Letters of the  Greek alphabet (e.g. α , β , θ ) are often used in trigonometry. When the same letter is used in two triangles, the understanding is that the two angles are equal. In the two triangles for the next question, ∠J = ∠X and ∠Y = ∠I.

An image of two triangles. Triangle IJK has one angle labeled alpha and one angle labeled theta. Triangle XYZ is much larger and also has one angle labeled alpha and one angle labeled theta.


Given the two triangles, ΔIJK and ΔXYZ, determine which of the following statements is true.
a. IJ corresponds to ZX and JK corresponds to XY
b. JK corresponds to XZ and YZ corresponds to IK
c. JK corresponds to XZ and IK corresponds to XY
d. JK corresponds to XY and IJ corresponds to XZ

Answer

b) JK corresponds to XZ and YZ corresponds to IK

An image of two triangles. The first triangle is labeled TUV with angles a and b and a sice of 10.8 cm labeled. The second triangle is labeled ABL and has angles a and b labeled as well as an 18.4 cm side and a 12.7 cm side.


Given the two triangles, ΔTUV and ΔABC, determine which of the following statements is true.
a. side TU is 21.6 cm
b. side TU is 5.1 cm
c. side TU is 7.5 cm
d. ΔTUV and ΔABC are not similar.

Answer

c) side TU is 7.5 cm. ΔTUV is a smaller triangle so the scale factor is between 0 and 1.

Δ ABC is used for the independent value and Δ TUV is used for the dependent values.

We can use the ordered pair (18.4, 10.8).

The scale factor or slope of the line is 0.59:

An image of the calculations required to determine the slope. m equals rise over run which means m equals 10.8 minus 0 over 18.4 minus 0. m is therefore equal to 0.59.

 The equation of the line is y = 0.59x.
Substitute the value, x = 12.7
y = 0.59(12.7)
y = 7.5 cm

An image of two triangles. The first triangle ABC has two side lengths labeled, they are 10.8 cm and 7.5 cm. The second triangle, labeled EFG, has one side length labeled as 15.7 cm.


If ΔABC ~ ΔEFG, which of the following statements is true?
a. The scale factor to determine FG is 1.45
b. The length of side FG is 18.3 cm
c. The equation to determine side FG is y = 2.1x where x is side lengths of ΔABC and y is the side lengths of EFG
d. The length of side EF is 17.9 cm

Answer

c The equation to determine side FG is y = 2.1x; AC corresponds to EG.
m = 15.7/7.5
m = 2.1
So y = 21.x

An image of a calculation showing m equals 15.7 over 7.5 which means m equals 2.1 so this means that y equals 2.1x.

This is the Portfolio icon. Triangle Information

In Activity 4 you created a document, Working with Triangles, where you listed the different variations for using the trigonometric ratios and the Pythagorean Theorem for solving problems.

An image of a table used to keep track of new information related to triangles. The table includes column headers that identify name of trigonometry relationship, algebraic expression, walue that need to be determined and values needed to solve for the unknown value.


You have added information for each trigonometric ratio and the Pythagorean Theorem.

The Pythagorean Theorem was used in an example with an isosceles right triangle.

How can this be added to your listing of variations?

Finding the height of an object by measuring the length of its shadow was an example in Activity 4 and is an example in this activity also.

In Activity 4, the solution used a trigonometric ratio and in this activity the solution uses a proportion, ratio table or the equation of a line. Notice the difference in the information that is used in each case.

What value(s) must be included to use a trigonometric ratio that you do not see used in a similar triangle ratio?

Add a section to your chart that discusses the methods to solve for side lengths in similar triangles.

Similar triangles may or may not be right triangles. Include in your description:

  • One pair of corresponding side lengths;
  • One known side length in one triangle;
  • When you can determine the length of the third side.
Go To Portfolio
 
 

This is the dropbox icon. Triangle Questions

Complete the questions in the document U2A8 Triangles.

Submit Your Work

 
Consolidation

CONSOLIDATION

You have been working with similar triangles. You have been introduced to some new notation.

  • The use of Greek letters to say that two angles are equal
  • The symbol, ~, which is used to say that two triangles are similar

You also revisited skills that you have learned in previous activities and used them to determine lengths of unknown sides in similar triangles. You worked with:

  • A scale factor greater than 1
  • A scale factor between 0 and 1
  • Slope of a line
  • Equation of a line that represents a proportional relation
  • Pythagorean Theorem
 

This is the dropbox icon. Journal Reflections

Open your document U2 Reflections.

Reflect on using linear equations, proportions and ratio tables to solve problems with similar triangles.

Which method do you prefer to use? Why? What do you need to learn to be more comfortable using the other methods?

Choose two sentence stems to lead your reflection today.

Submit Your Work

 
 

 

test text.