In previous activities, you reviewed solving equations and you used your algebraic skills to write the equation of a linear relation and to determine slope and x- and y-intercepts.

What does it mean to ‘solve for x’?

How does solving a linear equation relate to the graph of a linear relation?

Reading an Ordered Pair on the Graph of a Linear Relation

Earlier in your mathematics education, you would have been asked to determine ordered pairs on a graph of a relation. For example, you may have been given the graph of a linear relation such as y = 2x + 3.

If you had to determine the value for y when x equals 3, you would go to value of 3 on the x-axis and move vertically upwards to the graph of the line.

From there you would move horizontally left to the y-axis and read the value 9. You know that when x equals 3, y equals 9. You may also have stated that the point on the linear relation is (3, 9).

Similarly you may have been asked to determine the value for x when y is -7. This time you would go to the value -7 on the y-axis and move horizontally left to the graph of the line.

From there you would move vertically up to the x-axis and read the value -5. When y equals -7, x equals -5 or the point on the line is (-5, -7).

Reading a graph in this way will help you use graphs to solve linear equations.

Solving a Linear Equation Using a Graph

On the graph of y = -2x + 4, you can locate the value 8 on the y axis and then move horizontally to meet the line. This is the point on the line where y = 8.

You can determine the x value at this point. Move vertically to the x-axis and read the value, x = -2. This means that x = -2 when y = 8 for the relation, y = -2x + 4 and a point on the line is (-2, 8).

Solving the linear equation, -2x + 4 = 8, using algebraic skills yields the same answer, x = -2.

On this grid, notice that both the linear relation, y = -2x + 4, and the linear relation, y = 8, are graphed. When you determine the x coordinate at the point, you traced vertically to read the value,  x = -2. This vertical line is defined by the equation, x = -2. 

When you look at a linear equation in this manner, you can see that the solution, x = -2, is at the intersection of the linear relation, y = -2x +4 and the horizontal line, y = 8.

You can check that this is correct by substituting the value, x = -2 into the equation.

-2x + 4 = 8

LS = -2x + 4

      = -2 ( -2) + 4

      = 4 + 4

      = 8

RS = 8 so the value that is read from the graph is correct.

Using the same relation, y = -2x + 4, use the graph to determine the solution to -2 = -2x + 4.

You can see both linear relations, y = -2x + 4 and y = -2 graphed on the grid.

At the point of intersection, you can add in the vertical line, x = 3 which is the solution to the equation, -2 = -2x + 4.

You can check the solution in the original equation.

LS = RS so the solution is correct! You were able to read the value from the graph.

What you have just done is an example of the Mathematical Process of Connecting.

You are just beginning to look at problems that involve finding common solutions between two linear equations at the same time.

You  are doing this the way mathematicians would, by building from what you already know, graphing linear relations and solving linear equations.

Using the same relation, y = -2x + 4, use the graph to determine the solution to -2x + 4 = -7.

You can see both relations, y = -2x + 4 and y = -7 graphed on the grid. The point of intersection of the two lines is not at a spot where the lattice lines of the grid intersect.

In this situation, you can estimate the value for x and then check the value algebraically, as usual. At the point of intersection, you can estimate that x ≈ -7. Note that the symbol ≈ is used to indicate “is approximately equal to”.

Check in the original equation.

The LS does not equal the RS so the solution, x = 5.6, is not accurate. It does seem close, however, since -7.2 is close to -7.

Before you go any further, think about which way you would go to get a better estimate - to a number larger than 5.6? Or smaller than 5.6? Anticipating what should work is a valuable problem solving strategy.

Perhaps you were thinking that -7.2 is smaller than -7, so you need to take less away from +4? In that case, you might try 5.5, since it will give you a smaller negative number to  add to +4 .

You can solve the equation algebraically to provide an accurate solution.

Checking this solution, shows that x = 5.5 is the correct value.

You can see that an algebraic process will yield an exact, not an approximate value for a solution to an equation. The graphical process provides a visual picture of the solution. When you work with any relation in mathematics and have an equation to solve (determine the value for x or some other unknown), a graph of the relation and the horizontal line for the y value can be visualized to see the place(s) where the horizontal line crosses the relation’s line.

In the Minds On, you saw that solving linear equations can be shown graphically by rewriting the one equation (e.g. 2x + 3 = 9) as two linear relations (i.e. y = 2x + 3 and y = 9). In the examples, one linear equation is written in slope y-intercept form with a slope value that is neither 0 nor undefined and the other equation is a horizontal line, y = b, where b is the given y value. The solution to the equation is the value of x at the point of intersection.

System of Equations

In mathematics, when you work with 2 or more relations at one time and look for the common point(s) between the relations, you are working with a system of equations. When the relations are linear relations, it is called a linear system.

You will continue to work with a linear system and find the point of intersection both graphically and algebraically. The process of determining the point of intersection (the solution) of a linear system is called “solving a system.” The solution to a linear system has both an x and y value. 

The examples below will include both a graphical solution and an algebraic solution. By using graphing software, the point of intersection can be more accurately determined.

Solving a system by substitution

Example 1

Find the point of intersection of the linear relations y = -2x - 5 and y = 2/3x + 3.

Graphical solution:

1. Using desmos online calculator, graph each linear relation.
    

   

2. Select one of the linear relations by clicking on the line or clicking on the box where the equation is written.  A point appears where the lines cross, and if you hover over the point the ordered pair is displayed.

   

3. The point of intersection is (-3, 1), which can be checked in each linear relation.
4. Check.

Check that (-3, 1) is a point on each line (i.e., Check that x = -3 and y = 1 satisfies (definition:A point satisfies an equation when substituting in the values makes the left side equal to the right side of that equation.) each of the equations).

Algebraic Solution

In the Minds On, you saw that solving the linear equation -2x + 4 = 8  could be done graphically by using two linear relations, y = 8  and y = -2x + 4. You treat the left side and right side of the equation as individual relations.

When you are solving linear systems, you start with two equations, and your goal will be to combine them into a single equation that can be solved using the methods you already know. 

The question is to solve the system of two linear equations:

y = -2x - 5

y = 2/3x + 3

Each side of the equals sign has an expression. Since we are looking for a point that is common to both equations, the y-value is the same at that point.

Since the y-values are equal, we can substitute y = -2x - 5 for the y in y = 2/3x + 3.

Rewriting as an equation to solve looks like

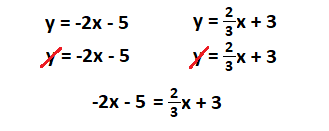
where you can solve for the value of x. Recall that you solved equations similar to this in the previous unit.

Since the question asked for the point of intersection of the two lines, you must determine the value for y by substituting the value determined for x into one of the equations.

If we use y = -2x -5, we get

y = -2(-3) - 5

y = 6 - 5

y = 1

To verify that you have not made an error in determining the point of intersection, check the ordered pair (-3, 1) using the other equation.

Use y = ⅔ x + 3

y = ⅔ (-3) + 3

y = -2 + 3

y = 1

Now that you have established that the point, (-3, 1) is a point on both linear relations, it is the one point that they have in common and is the point of intersection.

The process that you followed to do this is called “solving by substitution” - you replaced ‘y’ in one relation with the expression for ‘y’ from the other relation. You started with 2 equations written in slope y-intercept form so you had an expression for y in each equation. You represented it as a linear equation where you can solve for x. You started with two equations with the two variables, x and y, and through substitution created one equation with one variable.

Different Forms of Linear Relations

You have seen that linear relations can be written in two forms other than the slope y-intercept form (ex.: y = 3x - 7). The equation for a linear relation may also have the form 2x + 3y = 12 or 5x - 3y - 15 = 0.

The process of solving a linear system by substitution will look different depending on the form(s) you are given. To “solve by substitution” requires that you have at least one of the linear relations written so that one variable, either x or y, is isolated on one side of the equals sign. In the following examples, you will see one example where y is isolated and another example where x is isolated. The solution will be determined algebraically and then verified algebraically and graphically.

As you follow the algebraic solution for Examples 2 and 3, refer to the steps you  wrote in your Portfolio and modify them as needed to include the different variations.

Example 2

Find the point of intersection of the linear relations, y = 2x + 1 and 3x + 2y = 16.

Notice how y is isolated on one side of the equal sign: y = 2x + 1

We can substitute the expression (2x + 1) for y into 3x + 2y = 16.

3x + 2(2x + 1) = 16

 

Solve for x. I see that I have to multiply each term in the bracket by the factor 2 in front of the bracket:  2(2x + 1) = 2(2x) + 2(1).

Substitute x = 2 into one of the two linear relations to solve for y.

y = 2x + 1

y = 2(2) + 1

y = 4 + 1

y  = 5

Based on this work, it appears that the point of intersection is (2, 5).

Verify algebraically that (2, 5) is a point on the second linear relation. Substitute 2 in for x and 5 in for y.

3x + 2y = 16

LS = 3x + 2y

LS = 3 (2) + 2 (5)

LS = 6 + 10

LS = 16

And we know that RS = 16.

Recap: One linear equation with one variable was created from two linear relations to determine the point of intersection of the 2 linear relations. The equation was solved and it was determined that the point of intersection occurs when x = 2. One relation, y = 2x + 1, was used to determine the value for y at the point of intersection. The ordered pair, (2, 5) was verified to be a point on the line, 3x + 2y = 16.

The ordered pair (2, 5) is a point on each linear relation and so it is the point of intersection.

Verify graphically that (2, 5) is the point of intersection.

Check the graph using desmos.

Example 3

Find the point of intersection for the linear system 4x - 7y = 20 and x - 3y = 10.

The right side will be the simplest to isolate a variable since the coefficient of x is 1.

x - 3y = 10

Isolate the variable x in this linear relation.

x - 3y = 10

x - 3y + 3y = 3y + 10

x = 3y + 10

Substitute the expression (3y + 10) for x in 4x - 7y = 20.

4x - 7y = 20

4(3y + 10) - 7y = 20

Solve for y.

I see that I have to multiply each term in the bracket by the factor 4 in front of the bracket:  4(3y + 10) = 4(3y) + 4(10).

Substitute y  = -4 into one of the two linear relations to solve for x.

x - 3y = 10

x - 3(-4) = 10

x + 12 = 10

x + 12 - 12 = 10 - 12

x = -2

Based on this work, it appears that the point of intersection is (-2, -4).

Verify algebraically that (-2, -4) is a point on the second linear relation. Substitute -2 in for x and -4 in for y in the other equation.

4x - 7y = 20

LS = 4x - 7y

LS = 4(-2) - 7(-4)

LS = -8  + 28

LS= 20

And we know that RS = 20.

Recap: One linear equation with one variable was created from two linear relations to determine the point of intersection of the 2 linear relations. The equation was solved and it was determined that the point of intersection occurs when y = -4. One relation, x - 3y = 10 was used to determine the value for x at the point of intersection. The ordered pair, (-2,-4) was verified to be a point on the line, 4x - 7y = 20.

The ordered pair (-2, -4) is a point on each linear relation and so it is the point of intersection. 

Verify graphically that (-2, -4) is the point of intersection.

Check the graph using desmos. 

Practice Problems

Indicate which step you might see in the solution for the following linear system:

3x + 2y = 6
x + y = 4

a. 3(y + 4) + 2y = 6
b. 3(4 - y) + 2y = 6
c. 3(y - 4) + 2y = 6
d. 3(4 - x) + 2y = 6

Answer

Indicate which step you might see in the solution for the following linear system:

3x + 2y = 6
x + y = 4

a. 3x + 2y = x + y
b. 3x + 2(x + 4) = 6
c. 3x + 2(x - 4) = 6
d. 3x + 2(4 - x) = 6

Answer

What is the solution for the following linear system?

3x + 2y = 6
x + y = 4

a. (-2, -6)
b. (6, -2)
c. (-2, 6)
d. (2, -6)

Answer

Indicate which step you might see in the solution for the following linear system:

4x - y = 12
-5x + 3y = 6

a. -5(12 - y) + 3y = 6
b. -5x + 3(4x - 12) = 6
c. -5x + 3(12 - 4x ) = 6
d. -5(y - 3) + 3y = 6

Answer

Indicate which step you might see in the solution for the following linear system:

4x - y = 12
-5x + 3y = 6

a. -5x + 3(-6) = 6
b. 4x - 6 = 12
c. 4x - (9/2) = 12
id. 4(6) - y = 12

Answer

What is the solution for the following linear system?

4x - y = 12
-5x + 3y = 6

a. (-6, 12)
b. (-6, -12)
c. (6, 12)
d. (-12, -6)

Answer

 

Congratulations, you have completed Unit 3, Activity 2. You may move on to Unit 3, Activity 3.