In the previous activity, Activity 4, you looked at some of the laws of arithmetic and algebra that are related to multiplication. You worked with the zero product law and saw the connection between the law and finding the x-intercepts when you have the factored form of the equation for a quadratic relation.

In this activity, you will continue to work with the 2 forms for quadratic relations; the expanded form (standard) form y = x² + bx + c and the factored form y = (x-r)(x-s). The focus will be the change from the linear factors ((x-r) and (x-s)) to the expression in expanded form (x² + bx + c).

There is another law that involves connecting multiplication with addition that we will explore before working with the algebraic form of the equations.

The Distributive Law that involves both addition and multiplication states:

squareTilesAnimation

Long Description

You can see on the left that there are 4 rows where each row has 2 red blocks and 4 blue blocks.

On the right there are 4 rows of 2 red blocks and 4 rows of 4 blue blocks.

The 4 has been distributed to the red blocks and to the blue blocks.

Stating the law numerically looks like 4 x (2 + 4) = 4 x 2 + 4 x 4.

Let’s check that both sides of the equal sign have the same value.

Either way we do the calculation, we still get 24.

Since any numbers can be used in the law, you will often seen it written in the form:

a x (b + c) = a x b + a x c, where a is distributed across the b + c. It can also be written as a(b + c) = ab + ac since the multiplication signs are not required between the variables or before the bracket.

For further study, view the follownig video that further explains the distributive law:

Complete the practice questions at the end of the video.

Which of the following is a correct way of using the distributive property with 17 x 8? There may be more than one answer.
a. 17 x 8 = 15 + 2 x 8
b. 17 x 8 = 15 x 8 + 2 x 8
c. 17 x 8 = 10 x 8 + 7 x 8
d. 17 x 8 = 17 x 5 + 3

Answer

Which of the following is a correct way of using the distributive property with 13 x 27? There may be more than one answer.
a. 13 x 27 = 13 x 22 + 5
b. 13 x 27 = 10 + 3 x 27
c. 13 x 27 = 10 x 27 + 3 x 27
d. 13 x 27 = 13 x 20 + 13 x 7

Answer

The distributive law can be applied more than once if needed to simplify multiplication.

There are 13 rows and 14 columns.

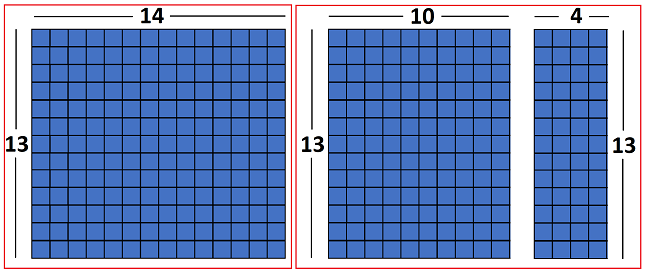
To multiply 13 x 14, 14 is split  to 10 + 4 and 13 is shown beside each block or distributed to both values (horizontal).

You can see the two pieces now - each block has the same number of rows and there are 10 columns in the larger block and 4 columns in the smaller block.

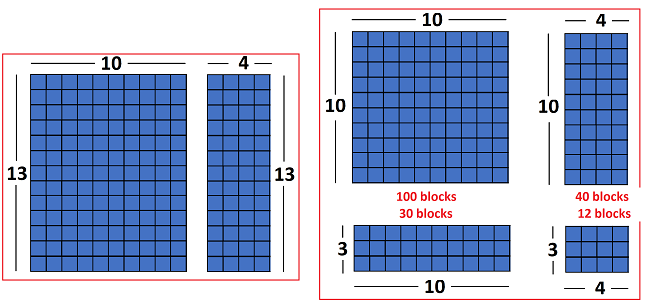
Next, 13 is split to 10 + 3 and  the distributive property is applied vertically as 10 is distributed to 10 and 3 and 4 is distributed to 10 and 3.

You can see the four pieces now -  two blocks have 10 columns and 2 blocks have 4 columns. Notice that the largest block is 10 x 10 and the one below is 3 x 10. Beside you can see the block that is 10 x 4 and the last block that is 3 x 4.

Notice that you need to multiply the length and width for each block before you add to get the total.

The total number of blocks is the sum of the blocks 100 + 30 + 40 + 12 = 182.

Both factors, 13 and 14, were decomposed to the sum of two numbers, 13 = 10 + 3 and 14 = 10 + 4.

When decomposing, we chose a "friendly" number, like 10, but we could have used other numbers. In fact, Sri used 5 and 9 for 14 and 10 and 3 for 13. Try it. See that is still works.

Many people use this method of decomposing numbers to turn a difficult multiplication question in a simpler question.

We could rewrite the original multiplication using the decomposition (definition:splitting a value into the sum of two numbers) of each factor.

13 x 14 = (10 + 3) x (10 + 4)

Did you know that the multiplication sign is not needed with the brackets. This would be the same if it was written as (10 + 3)(10 + 4):

13 x 14 = (10 + 3)(10 + 4)

             =  10 x 10 + 3 x 10 + 10 x 4 + 3 x 4

             = 100 + 30 + 40 + 12

             = 182

Notice that we have been using a rectangle to model multiplication. You are using the formula for finding the area of a rectangle which is length times width. This is often referred to as the area model for multiplication.

The area model is also used to illustrate the distributive law since it provides a picture of what is happening. You can see the original rectangle separated into the 4 smaller rectangles. The length and width of each smaller rectangle come from the values used to decompose the initial length and width. The area of the 4 rectangles is the same as the area of the original rectangle.

Complete the practice questions below, drawing the rectangles to verify the four zones.

Multiply 23 x 17 using the area model and the distributive law.

Answer

What is looks like in pictures:

Multiply 43 x 22 using the area model.

Answer

You worked with the area model for multiplication of numbers. You will use the same area model to manipulate the two forms of the expression for a quadratic.

Area Model and Quadratic Expressions

You learned to identify the information in each form of the equations for quadratic relations. If you are given the factored form of the equation, ( y = (x - r)(x - s))  you noticed that the zeros or x-intercepts could be read from the factors and the equation for the axis of symmetry could be found using the values for the x-intercepts. You also know that the y-intercept is the constant value c in the standard form, which is y = x² + bx + c.

In the Minds On, you used the area model and the distributive property to simplify multiplication. In this activity you will extend your use of the distributive property and use it with the factored form of a quadratic equation. Initially you can think about the factors as being the length and width of a rectangle. When you multiply length times width and determine area, you are describing the same rectangle in a different way. Similarly, when you apply the distributive property to the factored form you will have a different way to represent the same relation; this representation is the standard form of the quadratic equation.

Let’s look at this using a pictorial representation with tiles and make connections to the other representations that have been used in Units 1 and 2. You will explore the area model using the equation y = (x + 1)(x + 3).

Watch the following video, that goes over Distributive Property with Linear Factors:

A general tile representation can be used in place of all the individual tile pictures initially shown. This one picture using ‘x’ can replace the pictures that use specific values for x. Each area is labelled with its contribution to the total area of the rectangle. The 4 terms in the total area are added together, combining the like terms 3x and 1x (3x + 1x = 4x), to be simplified to the 3 terms in the standard form.

In the starting quadratic relation, y = (x + 3)(x + 1), the dependent variable, y, represents the total area and the factors (x + 3) and (x + 1) represent the length and width of a rectangle. When we multiply the length times the width, we determine an expression for total area, x2 + 4x + 3. The quadratic relation, y = x2 + 4x + 3 is the standard form for the same relation. We have changed the factored form to the standard form.

We can graph this relation, either in its standard form or in its factored form, and see that either equation will produce the parabola shown.  Some points are labeled on the parabola; y-intercept at (0, 3), the x-intercepts at (-1, 0) and (-3, 0) and the ordered pairs (1, 8), (2, 15) and (3, 24) which correspond to the values in the table of values or the tile pictures in the video.

You are using the area model to support your understanding of an algebraic method. As discussed in Unit 1, physical models have their limits - they can go only so far. (e.g. Some models only work with whole numbers, not fractions).

In the physical world, length, width and area are positive values. Look at the graph for the relation that you explored.

• When is the area not a positive value?
• When is the length or width a negative value?
• When are both the length and width negative values and what is the area? Does this really make sense in the physical world?

The area model is a tool that allows you to have a picture to generalize an algebraic process of multiplying linear factors whether or not the linear factors are lengths. You will return to this topic later.

See the summary sheet that includes all the models and information about the quadratic relation, U3A5 Summary Example.

As you continue with the activity, you will focus on the different algebraic forms for quadratic relations and the methods to change from one form to the other. This will provide the skills needed to extract different information from the algebraic model that is being used to describe some application of mathematics in the real world.

Expand Linear Factors (where the coefficient of x is 1) and Simplify Quadratic Expressions

When you are “expanding” the factors of a quadratic expression, you are multiplying the two linear factors and writing the quadratic expression.  You are using the area = length times width model to do the multiplication.

Open the applet to explore multiplication of two linear factors where the coefficient of x is 1.

At the top of the page, notice the multiplication of two linear factors and the equivalent quadratic expression represented in standard form.

In this picture, the linear factors are x + 5 and x + 3 and the quadratic is  x2 + 8x + 15.

The area model is shown. The blue and yellow tiles in the area model show the results of multiplying the two linear factors.

Use the the example in the image above to answer the following questions:

x + 3 is the:
a. horizontal side length of the rectangle.
b. vertical side length of the rectangle.
c. area of the rectangle.

Answer

x + 5 is the:
a. horizontal side length of the rectangle.
b. vertical side length of the rectangle.
c. area of the rectangle.

Answer

x² + 8x + 15 is the:
a. horizontal side length of the rectangle.
b. vertical side length of the rectangle.
c. area of the rectangle.

Answer

The blue tiles show the:
a. terms that involve x.
b. terms that only involve a constant but no x.

Answer

The yellow tiles show the:
a. terms that involve x.
b. terms that only involve a constant but no x.

Answer

To the right of the colourful area model is another example of the area model. This is a different version that does not use the tiles but which still shows the multiplication of the two linear factors. The four tile areas correspond to the four areas within the rectangle.

Algebra tiles are a useful tool in creating a picture to represent algebraic expressions and manipulations. There are three standard tiles - a unit tile which is a 1 by 1 tile, an x tile (rectangular) that is a 1 by x or x by 1 and and x2 tile which is an x by x tile. In the applet, blue is used to represent x and x2 and yellow represents 1. Notice that the linear factor, x + 3, is represented with one x-tile and 3 unit tiles.

You can explore the use of the applet using the practice questions below. Use the algebra tile template, to record your exploration. The example from the applet has been completed using the template. You can use this image as an example of how to use the template. Note that the factors are included as the length and width along the edges. Save the page in your notebook.

Expand and simplify.

• When you expand, you are multiplying the two linear factors and filling in the area within the frame with tiles. You are rewriting in area form.
• When you simplify, you are adding x-tiles (the “like terms”) and rewriting the whole expression.

For example, (x + 4)(x + 5) can be expanded and simplified to x² + 9x + 20:

For example, (x + 1)(x + 2) can be expanded and simplified to x² + 3x + 2:

For example, (x + 3)(x + 4) can be expanded and simplified to x² + 7x + 12:

For example, (x + 1)(x + 3) can be expanded and simplified to x² + 4x + 3:

All the examples have involved only addition in the factors. The next examples will include factors with subtraction. The x term will continue to have a coefficient of positive 1. You will no longer be able to use the applet since it cannot be used with subtraction.

Algebra tiles create a concrete model of algebraic expressions and are a great way to see the mathematics that you are doing.  You can continue to use the algebra tile template U3A5 Algebra Tile Template if you use different colours. Traditionally, we use blue for 1, x, and x2 and red for -1, -x, and -x2.

There is a website with algebra tiles that you can use. Open this demo which will allow you to get comfortable with using the algebra tiles online.

Watch the short video for instructions on using the online algebra tiles and general information about using algebra tiles.

Expand (x + 2)(x + 3) using your choice of model. Check to see the correct expansion with each model.

This is the collection of the 4 tile diagrams that represent the expansion you did yourself as well as the 3 examples from the videos.

They can be referred to as you update your observations in Patterns in Expanding.

Expand Linear Factors (including different coefficients of x) and Simplify Quadratic Expressions

You have established that the area model can be used to multiply or expand linear factors where x has a coefficient of 1. Along with the exploration, you also noted some patterns between the linear factors and the quadratic expression.

In this section, you will expand linear factors where the coefficient of x is not always 1.

Example: Expand and simplify the following:

(2x + 1)(3x + 2)

Remember:

• When you expand, you are multiplying the two factors and filling in the area within the frame with tiles. You are rewriting the expression in area form.
• When you simplify, you are adding like x tiles or matching zero pairs and rewriting the expression in “simplified” form.

Consider your observations of the expansion of linear factors earlier:

• What is different?
• How will the differences be reflected in the final quadratic expression?

Use the algebra tile frame to set up the question:

(2x + 1)(3x + 2)

Multiply the x terms together.

There are 2 columns and 3 rows of x so we get 6x²:

Multiply the two pairs of constant terms and x terms:

1 times 3x = 3x and 2 times 2x = 4x.

This is 3x + 4x = 7x.

Multiply the constant term times the constant term:

1 x 2 = 2

Add the three sections together:

(2x + 1)(3x + 2) = 6x² + 7x + 2

You probably noticed that the coefficient of x in each of the two linear factors has an influence on the number of x² and x tiles in the quadratic, but that the coefficient of x does not influence the value of the constant.

Watch the follownig video for another example using tiles:

Example:

Rewrite in area form. Simplify the expression.

(3x - 2)(2x + 5)

To create the area model for this question, how many x² tiles will be needed? How many x-tiles will be needed? Will they be positive or negative tiles?

As the number of tiles increases, it can become more difficult to create the tile model simply because of the number of tiles required. Recall the first interactive with the positive tiles only. There was an alternate area model (a 4 quadrant box) with the algebraic expressions written in place of the tiles. For the questions requiring a larger number of tiles, you can use this alternate area model.

To use this area/box model, write one factor along the top and the other factor on the side as if you are placing tiles. As with the tiles, multiply the side lengths to determine the area for each section of the box.

Why are the terms in the top right and lower left always like terms? 

Practice

Rewrite the following in area form. Simplify the expression.

1. (x - 5)(2x + 3)
2. (4x - 1)(5x + 3)
3. (2x - 5)(3x - 1)
4. (2x + 1)(2x + 1)
5. (3x + 2)(3x - 2)

When complete, check your answers.

Connecting Algebra with the Graphs

When you were expanding and simplifying the multiplication of two linear factors, you were really just practicing algebra. The expressions had only one variable, x. The skills you have developed become very important when you are trying to analyse the relationships between two different quantities as one of them changes - the independent and the dependent variables. This is what you are doing when you analyse a quadratic relation. In this next section, you will apply what you know about changing forms of quadratic expressions to analyse quadratic relations.

In this graph, you can see that the parabola crosses the x-axis at approximately -3 and 5. This means that the quadratic has factors (x + 3) and (x - 5).

To check if y = (x + 3)(x - 5) is the equation for this graph, you really need to check with a third point. Perhaps you noticed that the y-intercept appears to be -15. By substituting the value x = 0, the value of x at the y-intercept, you can check that the equation is a match for the graph.

y = (x + 3)(x - 5)

y = (0 + 3)(0 - 5)

y = 3 x -5

y = -15.

When x = 0, y = -15 so the equation matches the graph. Success!

The equation for a relation describes the connection between the independent and dependent variables. It can be used to determine ordered pairs to create a graph of the relation. Different forms of the equation for a quadratic relation can be used to identify the key features of the relations. 

Using an equation, you can identify the y-intercept and the slope of a linear relation (straight line) and now you can identify the zeros (or x intercepts) of a quadratic relation (parabola) from its factored form. You have been using an area model to convert the factored form into the standard form. From the standard form, you can identify the y-intercept.

The area = length times width model is useful as it creates a physical picture of the algebraic manipulation that you are learning to use to create equivalent forms of a quadratic relation. You used the area model to look at the patterns that exist between the linear factors and the quadratic expression that results from the multiplication (expand and simplify).   

In Activity 4, you completed two Frayer models. One focused on the standard form of the quadratic relation and the other focused on the factored form of the quadratic relation. You have seen more connections between the two forms in this activity. You can return to the Frayer models and add additional detail.

Congratulations, you have completed Unit 3, Activity 5. You may move on to Unit 3, Activity 6.