When a force is applied to an object, the result is typically an acceleration in the direction of the net force. By making an object accelerate, we are changing the amount of energy it has. Energy is the ability to do work or accomplish a task.

By applying a force on a ball when we throw it, we are giving it the ability to travel through the air, and the ability to make a dent in the dirt when it lands. The ball would not have been able to do those things without the transfer of energy from your hand to the ball.

It is easy to imagine that the bigger the initial force on the ball, the greater the amount of energy it has - the farther it will be able to travel through the air, or the deeper the dent it will make in the dirt when it lands. Indeed, the huge force used by a bow to accelerate an arrow gives the arrow enough energy to embed itself deep within a target.

In this activity, we will be looking at different types of energy, and how we can measure the transfer of energy from one object to another.

Work is the amount of energy transferred to an object when it experiences a displacement and is acted upon by an external force. We can write the equation for work as:

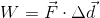
$W=\vec{F}\cdot \Delta \vec{d}$

Because force is measured in newtons, and displacement is measured in metres, work is measured in newton-metres. This unit is given a special name: joules (J). Note that although force and displacement are vector quantities, work is a scalar quantity. The vector notation disappears as a result of the dot operator (∙) used to multiply the two vectors. The symbol for work (W) is very similar to the symbol for weight (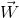 $\vec{W}$ ) - the difference being that weight is a vector quantity so we add the vector notation of the arrow, while work is a scalar quantity. Be careful to not mix up the two.

In this unit, we will only consider the cases where:

The external force and displacement are in the same direction, resulting in positive work that we can calculate by multiplying the magnitudes of the external force and displacement.
The external force and displacement are in opposite directions, resulting in negative work that we can calculate by multiplying the magnitudes of the external force and displacement, and adding a negative sign.
The external force is perpendicular (at a right angle) to the object’s displacement, resulting in zero work.

The dot operator (∙) makes the vector notation disappear when calculating the product of force and displacement to find work, and results in the positive/zero/negative work cases outlined above. There are other possibilities (for example, if the external force is at a 45 degree angle to the displacement) but we won’t consider those cases in this unit.

If the positive/zero/negative rules do not seem intuitive, try thinking about a skater on an ice surface (which we will assume is frictionless):

If the skater is initially at rest (not moving) and someone pushes them (this is the external force), they will start to slide forward in the direction of the push. The external force and displacement are in the same direction, and the skater gains energy (positive work) which we observe as an increase in speed.

If the skater is moving, and as they approach the boards surrounding the rink they extend their arms and push their hands against the boards, the boards push back on the skater’s hands (remember Newton’s 3rd law). This is the external force that acts to slow down the skater and hopefully prevent an injury. The skater’s displacement is forward, toward the boards, but the external force of the boards on the skater is in the backward direction. The external force and displacement are in opposite directions, and the skater loses energy (negative work) which we observe as a decrease in speed.

While the skater is gliding along, there are two other forces at work: the force of gravity pulling the skater toward the Earth, and the normal force of the ice on the skater, pushing them up. Since both of these forces act perpendicular to the skater’s displacement, they accomplish zero work. You can think of the skater gliding along at a constant velocity - their speed is not increasing or decreasing so no work is accomplished by either of these forces.

Friction on a Skater

In the real world, ice skating is a nearly frictionless activity, but there is still a little friction between the skate blades and the ice. Take a moment to reflect if work done by the force of friction on a gliding skater is positive, negative, or zero and explain your reasoning why. Record other examples of positive, negative, and zero work.

Join The Discussion

We can consider work accomplished by individual forces, for example someone pushing the skater forward while a small frictional force is working to oppose this motion, as well as net work accomplished by the net force acting on an object. This is two different ways of thinking about the same thing: we can either calculate the work done by each of the individual forces acting on an object and add those quantities up to find the “net work” or total change in the energy of an object, or, sum the forces acting on the object to find the net force, and multiply that net force by the object’s displacement to find the net work - two different ways to find the net change in energy of the object.

Let’s try a few questions involving work. Try each question yourself, and then follow along with the full solution to see if you are on the right track. After the sample questions, you will have a chance to try some on your own.

Example 1

A weightlifter lifts a 140 kg barbell 2.1 m [up] from the floor at a constant velocity. What is the work done by the weightlifter?

Solution

Given:

m = 140 kg

$\Delta \vec{d}=2.1m[up]$

Required:

We are being asked to determine the work done by the weightlifter on the barbell.

W = ?

Analysis:

Work is equal to the external force applied on the object multiplied by the displacement of the object. In order to determine the force, let us look at the free-body diagram for the barbell.

This is a free-body diagram of a barbell being lifted by a weightlifter at constant velocity.

Because the barbell is moving at a constant speed (not accelerating) during its upward displacement, the magnitude of the upward force of the weightlifter on the barbell must equal the magnitude of the downward force of gravity on the barbell. Once we calculate the force of gravity on the barbell (force of gravity, or weight, is the object’s mass times the gravitational acceleration), we will know the force the weightlifter is using to perform work on the barbell.

Lastly, because we are on Earth, we know $\vec{g}=9.8m/s^{2}[down]$ .

Solution:

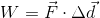
$W=\vec{F}\cdot \Delta \vec{d}$

In this case, the force doing the work is the force of the weightlifter on the barbell, which is equal to the gravitational force on the barbell.

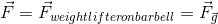
$\vec{F}=\vec{F}_{weightlifter on barbell}=\vec{F}_{\vec{g}}$

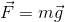
$\vec{F}=m\vec{g}$

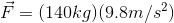
$\vec{F}=(140kg)(9.8m/s^{2})$

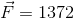
$\vec{F}=1372$

Note: We will use the unrounded calculated value for force to continue the calculation, and round at the end. Rounding intermediate results in the middle of a question would introduce “round off error,” which we want to avoid.

Therefore,

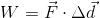
$W=\vec{F}\cdot \Delta \vec{d}$

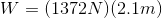
W=(1372N)(2.1m)

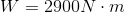
$W=2900N\cdot m$

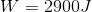
W=2900J

Paraphrase:

The weightlifter did 2900 J of work lifting the barbell.

Example 2

The driver of a 1575 kg car slams on the breaks, causing it to skid. The car comes to a stop after skidding for 25 metres. The coefficient of kinetic friction for rubber on asphalt is 0.97. What is the work done by the force of friction on the car? Ignore air resistance.

Solution

Given:

m = 1575 kg

$\Delta \vec{d}=25 m [up]$

μk = 0.97

Required:

We are asked to calculate the work done by the force of friction on the car.

W = ?

Analysis:

Work is equal to the force applied on the object multiplied by the displacement over which the force is being applied. In order to determine the force, let’s look at the free-body diagram for the car.

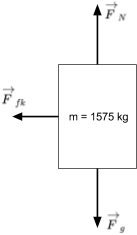
This is a free-body diagram for car skidding to a stop.

The only force acting to bring the car to a stop is the force of kinetic friction, which is equal to the coefficient of kinetic friction multiplied by the normal force. Because there is no acceleration in the vertical direction, the normal force and the gravitational force have the same magnitude. Once we calculate the kinetic friction force, we can use this to calculate the work done on the car.

Solution:

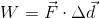
$W=\vec{F}\cdot \Delta \vec{d}$

In our case, the force doing the work is the kinetic friction force between the tires and the road, and the force is acting in the opposite direction to the car’s displacement, so the work will be negative.

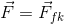
$\vec{F}= \vec{F}_{fk}$

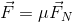
$\vec{F}=\mu \vec{F}_{N}$

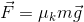
$\vec{F}=\mu_{k} m\vec{g}$

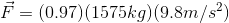
$\vec{F}=(0.97)(1575kg)(9.8m/s^{2})$

Therefore,

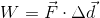
$W=\vec{F}\cdot \Delta \vec{d}$

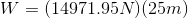
W=(14971.95N)(25m)

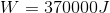
W=370000J

Paraphrase:

The force of friction did -370000 joules of work on the car.

Questions

Try the following questions on your own, and then check them to see how you did. Make sure you express each answer to the correct number of significant digits.

Lina pushes a box across the floor with a net force of 26 N. If she covers the length of the room (31 m), how much work has she done?
1. 1.2 J
2. 57 J
3. 810 J
4. 7900 J
Answer

c. 810 J

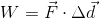
$W=\vec{F}\cdot \Delta \vec{d}$

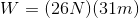
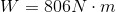
$W=806N\cdot m$

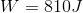
Gen lifts a 5.0 kg box from the floor to a shelf (2.1 m high) at a constant speed. How much work has he performed?
1. 1.1 J
2. 2.4 J
3. 11 J
4. 100 J
Answer

d. 100 J

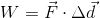
$W=\vec{F}\cdot \Delta \vec{d}$

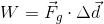
$W=\vec{F}_{g}\cdot \Delta \vec{d}$

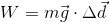
$W=m{\vec{g}}\cdot \Delta \vec{d}$

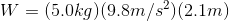
$W=(5.0kg)(9.8m/s^{2})(2.1m)$

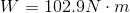
$W=102.9N\cdot m$

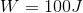
A machine does 5356 J of work in lifting an object 10.3 m at constant speed. What is the mass of the object?
1. 53.1 kg
2. 520 kg
3. 5096 kg
4. 55 200 kg
Answer

a. 53.1 kg

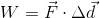
$W=\vec{F}\cdot \Delta \vec{d}$

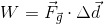
$W=\vec{F}_{\vec{g}}\cdot \Delta \vec{d}$

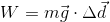
$W=m{\vec{g}}\cdot \Delta \vec{d}$

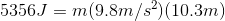
$5356J=m(9.8m/s^{2})(10.3m)$

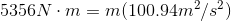
$5356N\cdot m=m(100.94m^{2}/s^{2})$

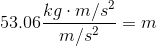
$53.06\frac{kg\cdot m/s^{2}}{m/s^{2}}=m$

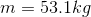
Police are investigating a crash where a driver may have hit a deer. By measuring the skid marks on the road, they know the car (of mass 1375 kg) was skidding for 16.8 m. If the coefficient of friction between rubber and dry concrete is 1.02, how much work was done by the force of friction to stop the car?
1. -17.1 J
2. -13 700 J
3. -23 600 J
4. -231 000 J
Answer

d. -231 000 J

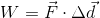
$W=\vec{F}\cdot \Delta \vec{d}$

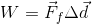
$W=\vec{F}_{f}\Delta \vec{d}$

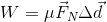
$W=\mu \vec{F}_{N}\Delta \vec{d}$

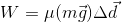
$W=\mu (m\vec{g})\Delta \vec{d}$

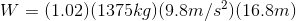
$W=(1.02)(1375kg)(9.8m/s^{2})(16.8m)$

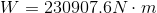
$W=230 907.6N\cdot m$

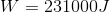
When the direction the force that is being applied is the same as the direction of the motion (like the weightlifter lifting a barbell), we call that positive work.

When the direction the force is being applied is the opposite to the direction of the motion (like the force of friction between skidding tires and the road causing a car to come to a stop), we call that negative work.

Net work is the total amount of work on an object. Like net force, in order to determine net work, we need to examine each source of energy transfer on an object in a given direction.

Read through the following example to see how to determine net work.

Example 3

This is an image of a pail of Hallowe’en candy that children might be tempted to fight over.

Three children are pulling on a bag of Hallowe’en candy, which moves 0.87 m to the left. Mishaal pulls with a force of 45 N [left], Shelley pulls with a force of 55 N [right], and Linda pulls with a force of 30 N [left]. What is the net work done on the bag of candy?

Given:

$\vec{F}_{Mishaal on bag}=45N[left]$

$\vec{F}_{Shelley on bag}=50N[right]$

$\vec{F}_{Linda on bag}=30N[left]$

$\vec{d}=0.87m[left]$

Required:

We are being asked to determine the net work on the bag of candy.

$W_{net}=?$

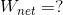
Analysis:

Net work is the total amount of work on an object, taking into account the direction of each energy transfer.

Solution:

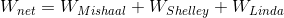
$W_{net}=W_{Mishaal}+W_{Shelley}+W_{Linda}$

Mishaal’s work:

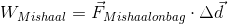
$W_{Mishaal}=\vec{F}_{Mishaal on bag}\cdot \Delta \vec{d}$

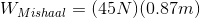
$W_{Mishaal}=(45N)(0.87m)$

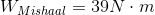
$W_{Mishaal}=39N\cdot m$

Mishaal’s work on the bag is in the same direction as the displacement of the bag - to the left. The work he does on the bag of candy is therefore positive.

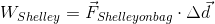
$W_{Shelley}=\vec{F}_{Shelley on bag}\cdot \Delta \vec{d}$

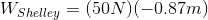
$W_{Shelley}=(50N)(-0.87m)$

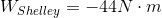
$W_{Shelley}=-44N\cdot m$

Shelley’s work on the bag is in the opposite direction as the displacement of the bag - to the left. The work she does on the bag of candy is therefore negative.

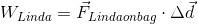
$W_{Linda}=\vec{F}_{Linda on bag}\cdot \Delta \vec{d}$

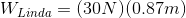
$W_{Linda}=(30N)(0.87m)$

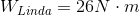
$W_{Linda}=26N\cdot m$

Linda’s work on the bag is in the same direction as the displacement of the bag - to the left. The work she does on the bag of candy is therefore positive.

Recall that a newton-metre is the same as a joule:

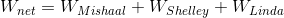
$W_{net}=W_{Mishaal}+W_{Shelley}+W_{Linda}$

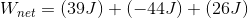
$W_{net}=(39J)+(-44J)+(26J)$

$W_{net}=21J$

Paraphrase:

The net work done on the bag of candy is 21 J. Because the end result is positive, we know that the net work was performed in the same direction as the bag’s displacement: to the left.

Is it possible for an individual force to do zero work?

If you can have positive work and negative work, it begs the question if it is possible to have a case where zero work is being done. It is indeed possible, but only under one of the following conditions:

You can have zero work if:

A force is exerted but there is no displacement
- Example: You pushing against a wall - no matter how hard you push, if the wall doesn’t move, you’ve done no work;
There is a displacement but no force is exerted
- Example: A rocket drifting through space;
A force is exerted in a direction perpendicular to the direction of the displacement
- Example: A mattress pushing down on the roof of a car that is travelling forward;

It is also possible to have zero net work being done on an object if:

Both positive and negative work is being done on an object, and they sum to zero
- Example: One person pulls on an object with a force of 10 N in one direction, while another person pulls on the object with a force of 10 N in the opposite direction. If the object is moving in either direction, both people will have done work on the object (one positive and one negative) but the net work done on the object is zero.

Think back to the weightlifter we watched at the beginning of this activity. In the reflection questions, we saw that he was doing no work while holding the weights overhead. Which of the above criteria for zero work is he fulfilling?

Reflection

Create a reflection to answer the following question. Consider using a diagram to help justify your answer.

Are the net force and the net work always in the same direction? Why do you think this?

Go To Portfolio

Power

You may have noticed that it does not matter how long a force has to be applied to move an object in order to calculate the amount of work being done. A person lifting a pile of books a height of one metre will do the same amount of work if they take one second to do it, or one minute. If we want to look at how much work is done per unit time, we look at power.

Because power is work per unit time, we can write:

$P=\frac{W}{\Delta \vec{t}}$

...where W is work in joules, and Δt is time in seconds. The units for power are therefore joules per second (J/s). Just like the joule is actually a newton-metre, we give joules per second a special name, too: a watt.

You may have seen watts before with respect to light bulbs - the power they consume is often given in watts. The more powerful the light, the higher the wattage, the more energy it consumes (and the brighter the bulb will be).

Let’s look back at our weightlifter example earlier in this activity. We calculated the work being done by the weightlifter to be 2900 J. How much power will the weightlifter have exerted if it takes 10 seconds to lift the barbell? How much power will be exerted if it takes 2 seconds to lift the barbell?

Given:

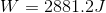W=2881.2J (the unrounded value, since we are continuing the calculation)

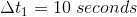
$\Delta \vec{t}_{1}=10\; seconds$

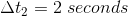
$\Delta \vec{t}_{2}=2\; seconds$

Required:

We are asked to determine the power of the weightlifter if it takes 10 seconds to lift the weight (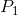 $P_{1}$ ), and the power of the weightlifter if it takes 2 seconds to lift the weight ( $P_{2}$ ).

$P_{1}=?$

$P_{2}=?$

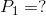
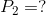
Analyse:

We know that power is the amount of work completed per unit time.

Power is measured in watts, which are joules per second.

Solution:

$P=\frac{W}{\Delta \vec{t}}$

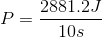
$P=\frac{2881.2J}{10s}$

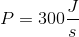
$P=300\frac{J}{s}$

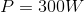
P=300W

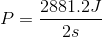
$P=\frac{2881.2J}{2s}$

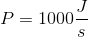
$P=1000\frac{J}{s}$

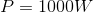
P=1000W

Paraphrase:

When the weightlifter lifted the weight in 10 seconds, they had a power of 300 watts. When the weightlifter lifted the weight in 2 seconds, they had a power of 1000 watts. The faster the weight was lifted, the greater the power exerted.

Other Units of Power

Depending on the context, we tend to use different units for power. You likely have seen watts as a rating of power on light bulbs. But when we talk about the power of an engine, or an air conditioner, or a physical exercise, we often use other units.

When James Watt (after whom the unit watt is named) invented the steam engine in the 18th century, he needed a way of comparing the power of the engine to the power of something most people would have been familiar with: a horse. He coined the term “horsepower,” which referred to the amount of work a horse could do (about 45 000 J) in one minute. Though there have been different standards in the past for how much a horse could pull, today one horsepower is approximately 740 W. Horsepower is still used when comparing power of engines of race cars or pickup trucks.

Heating and cooling systems use a different unit for energy called the British thermal unit, or Btu. A Btu is the amount of heat required to raise the temperature of one pound of water by one degree Fahrenheit. The power of heating and cooling systems is often given in Btu per hour, where one Btu/hr equals approximately 0.29 W.

Did you know it is possible to determine the power of a human?

Calculate YOUR Power!

In this task, you will perform three different physical activities, and calculate your power during each. How powerful will you be?

This is an image of people performing a box jump.

Choose any THREE of the following activities:

Pushup
Chin-up
Leg raise
Climbing a rope
Going up a flight of stairs
Lifting a heavy object
Activity of your choice, approved by your teacher

You may have noticed that each activity occurs in the vertical direction. This will make it easier for us to calculate power, as the force you exert will only be in the vertical direction. These will be approximations of the power you exert, as we recognize that there will be at least a little acceleration associated with each of the movements.

Remember that our formula for power is:

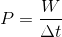
$P=\frac{W}{\Delta \vec{t}}$

And our formula for work is:

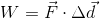
$W=\vec{F}\cdot \Delta \vec{d}$

We can therefore write:

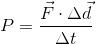
$P=\frac{\vec{F}\cdot \Delta \vec{d}}{\Delta \vec{t}}$

Since we are overcoming the force of gravity, we can use 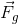$\vec{F}_{\vec{g}}$ in our formula as shown below. Note that this formula is a bit of a simplification. When climbing the stairs for example, you push down on the stair tread which results in a reaction force (remember Newton’s third law) of the stair tread pushing back up on you, allowing you to climb. In reality, the force that is doing the work is the force of your leg muscles acting on your bones. This is an internal force that transforms the shape of your body as you climb the stairs, but it is still doing work and the formula that is developed below will still calculate your power as you complete an activity.

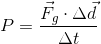
$P=\frac{\vec{F}_{g}\cdot \Delta d}{\Delta \vec{t}}$

$P=\frac{m\vec{g}\cdot \Delta d}{\Delta \vec{t}}$

So, in order to calculate your power in each activity, you will require the following measurements:

Mass (m) in kg (How much mass is being lifted?)
Displacement ( 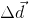$\Delta d$ ) in m (How far was the mass lifted?)
Time (t) in seconds (How long did it take to lift the mass?)

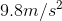Remember that $\vec{F}_{\vec{g}}$ is a constant, at $9.8m/s^{2}$ [down] (assuming you are doing these activities on Earth!).

Create a chart to track the data you collect. Use the GRASP method to calculate your power for each activity, remembering to paraphrase your solutions.

Answer the following questions,

During which activity did you have the most power?
During which activity did you have the least power?
In general, how could you increase your power in any activity?
Why would this task have been more difficult in the horizontal direction (i.e. calculating your power when running)?

Submit Your Work

Types of Energy

Energy can be classified into different types. In this unit, we will consider nine different types of energy. Some we describe only qualitatively, while with others we will learn to calculate specific numeric values.

Questions

See if you can guess how each type of energy is produced, and then carry on to read more about each type.

Type of Energy	Image
1. Chemical Potential	A.
2. Elastic Potential	B.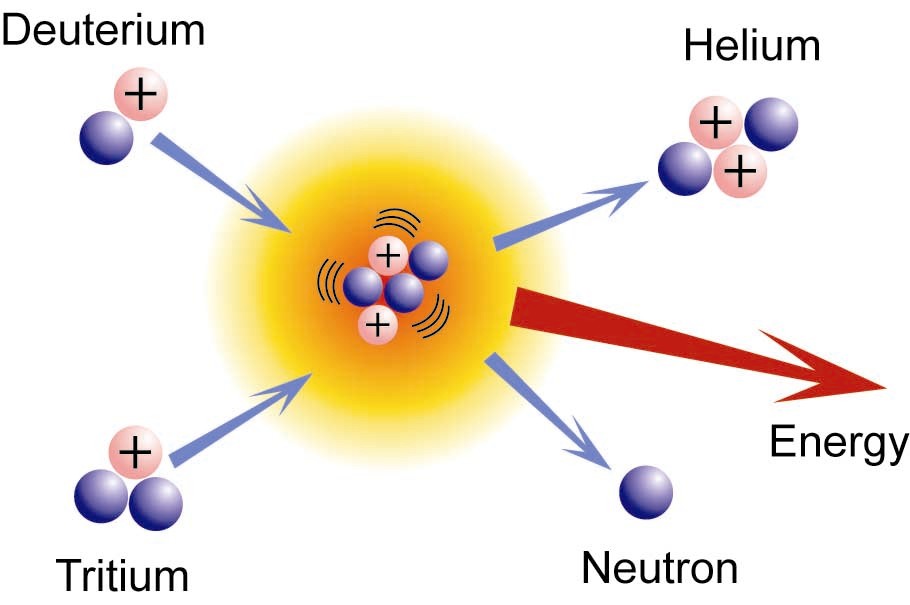 by chemwiki.ucdavis.edu
3. Electrical	C.
4. Gravitational Potential	D.
5. Kinetic	E. by
6. Nuclear	F.
7. Radiant	G.
8. Sound	H.
9. Thermal	I. by

Answer

Type of Energy	Image
1. Chemical Potential	D.
2. Elastic Potential	F.
3. Electrical	I.
4. Gravitational Potential	G.
5. Kinetic	H.
6. Nuclear	B.
7. Radiant	A.
8. Sound	E.
9. Thermal	C.

The nine types of energy we will be learning are:

Radiant Energy: The energy possessed by electromagnetic radiation. Radio waves, light, microwaves, and x-rays are all examples of radiant energy.

Nuclear Energy: The energy possessed by the nucleus of an atom, released during fission or fusion.

Kinetic Energy: The energy possessed by an object

CONSOLIDATION

Summary

Work: The amount of energy transferred to an object, by a force applied over a displacement. It is given a symbol of W, and is measured in joules (J).

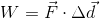
$W=\vec{F}\cdot \Delta \vec{d}$

Positive work occurs when the force and the motion are in the same direction.
Negative work occurs when the force and the motion are in opposite directions.
Net work is the total work that is done on an object.

Zero work can occur under one of the following circumstances:

An individual force is exerted but there is no displacement, or
There is a displacement but no individual force is exerted, or
An individual force is exerted in a direction perpendicular to the direction of the displacement, or
Both positive and negative work is being done on an object, and they sum to zero.

Power: The rate of doing work per unit time. It is given a symbol of P, and is measured in Watts (W).

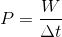
$P=\frac{W}{\Delta t}$

Energy: The ability to do work or accomplish a task. It is given the symbol E, and is measured in joules (J). While there are equations to calculate the energy in certain cases, in general,

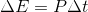
$\Delta E=P \Delta t$

Nine types of energy:

Radiant Energy
Nuclear Energy
Kinetic Energy
Thermal Energy
Sound Energy
Electrical Energy
Chemical Potential Energy
Gravitational Potential Energy
Elastic Potential Energy

Work, Energy, and Power
Work, Energy, and Power

MINDS ON

ACTION

Friction on a Skater

Example 1

Solution

Example 2

Solution

Questions

Example 3

Is it possible for an individual force to do zero work?

Reflection

Power

Other Units of Power

Calculate YOUR Power!

Types of Energy

Questions

CONSOLIDATION

Summary

Work, Energy, and PowerWork, Energy, and Power

MINDS ON

ACTION

Friction on a Skater

Example 1

Solution

Example 2

Solution

Questions

Example 3

Is it possible for an individual force to do zero work?

Reflection

Power

Other Units of Power

Calculate YOUR Power!

Types of Energy

Questions

CONSOLIDATION

Summary

Work, Energy, and Power
Work, Energy, and Power