Work, Energy, and Power
Kinetic Energy, Gravitational Potential Energy, and Thermal Energy

MINDS ON

Have you ever been on a roller coaster? There is something thrilling about slowly creeping up to scary heights, only to be “dropped” at high speeds and spun around a loopy track - sometimes even upside down!

Take a look at this first-hand view of the path the Fahrenheit Roller Coaster takes. One of the unique features of this ride is that the drop after the first hill is greater than 90 degrees - it actually curves back in the direction of the hill, making riders feel like they will come out of their seats!

Reflection

Take a few minutes to think about the video, and re-watch it as many times as you like. Create a reflection to record the answers to the following questions:

Which types of energy does the roller coaster have throughout its ride?
The roller coaster cars do not have engines to power their motion. Where does the roller coaster get all the energy it needs to complete the track?

Go To Portfolio

ACTION

Recall that work is the amount of energy transferred to an object when it experiences a displacement and is acted upon by an external force. It is given a symbol of W and is measured in joules (J).

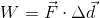
$W=\vec{F}\cdot \Delta \vec{d}$

We can use this formula to determine the work done by very specific forces, generating specific types of energy. We will examine three types of energy in this activity: gravitational potential, kinetic, and thermal. Before we start deriving equations for gravitational potential energy and kinetic energy, we should note that since work is the transfer and/or transformation of energy, we can also write its symbol as 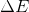$\Delta E$ .

Gravitational Potential Energy

In general, gravitational potential energy is the energy stored between any two masses, but in this course we consider the energy stored between the Earth and objects raised or lowered near the Earth’s surface. This simplifies things considerably and we can think of gravitational potential energy as the energy stored in an object due to its height above the ground. If you hold a ball at shoulder height, it remains motionless. However if you release it, even without pushing or throwing it, it begins accelerating, transforming the gravitational potential energy stored in the ball into kinetic energy in the form of the motion of the ball as it falls. Just as it hits the ground, it has no more gravitational potential energy, but it has reached its maximum downward velocity. Our course will not explore how the ball stops after it hits the ground.

The work being done on the ball as it falls is due solely to the force of gravity, so we can rewrite our work equation to reflect this. This work is a change in gravitational potential energy, 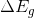$\Delta E_{g}$ .

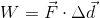
$W=\vec{F}\cdot \Delta \vec{d}$

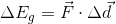
$\Delta E_{g}=\vec{F}\cdot \Delta \vec{d}$

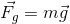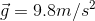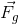Recall that the magnitude of the force of gravity is $\vec{F_{g}}=m\vec{g}$ , where $\vec{g}=9.8m/s^{2}$ [down]. Let’s substitute this in for $\vec{F_{g}}$ :

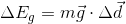
$\Delta E_{g}=m\vec{g}\cdot \Delta \vec{d}$

But what is the displacement (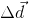 $\Delta \vec{d}$ ) of a falling object? In the case of the ball, it is the change in height of the ball above the ground. We label this as 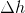$\Delta h$ , for the change in height. We can remove the vector notation because the force and displacement are in the same direction, resulting in positive work that is calculated as the product of these two quantities.

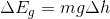
$\Delta E_{g}=mg\Delta h$

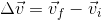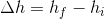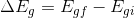Recall that we can write the change in a variable as the final value minus the initial value. We saw this with the change in velocity being the final velocity minus the initial velocity $\Delta \vec v= \vec v_{f}-\vec v_{i}$ . We can write the same for the change in height: $\Delta h=h_{f}-h_{i}$ and change in energy $\Delta E_{g}=E_{gf}-E_{gi}$ .

Let’s put these into our equation:

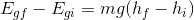
$E_{gf}-E_{gi}=mg(h_{f}-h_{i})$

We do not know the specific initial height for the object (that will depend on the context of the question), but if we set the final height to be at the same level as the ground, then hf becomes equal to 0 m. Recall that an object in contact with the ground has no gravitational potential energy relative to the ground, so 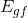$E_{gf}$ becomes equal to 0 J.

This image illustrates the difference in height of a ball above a surface.

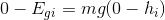
$0-E_{gi}=mg(0-h_{i})$

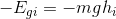
$-E_{gi}=-mgh_{i}$

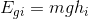
$E_{gi}=mgh_{i}$

So, the gravitational potential energy of the object at an arbitrary initial height relative to the ground is equal to the product of the mass of the object (m), the gravitational constant (g) and the height of the object relative to the ground. We can remove the subscript i and are left with our final equation for gravitational potential energy:

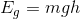
$E_{g}=mgh$

Notice that we removed the Δ from the energy - we are now calculating the amount of energy the object has stored by being above the ground, and not the change in energy as it falls (which will, when calculated, actually give the same amount, but it is still important to note).

Looking at the equation, we know that the gravitational potential energy of any object depends on three things:

The mass of the object, measured in kg;
The gravitational acceleration of the planet, in our case, ;
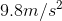The height of the object, measured in m.

Let’s practice with this equation. Try each question, and then check your answer against the solution provided.

Practice

Which has more gravitational potential energy: a 5.0 kg bowling ball suspended 2.0 m above the floor, or a 2.0 kg cinder block suspended 5.0 m above the floor? How do you know?

Solution

Given:

Case A Case B

m = 5.0 kg m = 2.0 kg

h = 2.0 m h = 5.0 kg

Required:

In both cases, we are asked to determine the gravitational potential energy, so that we can compare the two values.

$E_{g}= ?$

Analysis:

Gravitational potential energy is proportional to the mass of the object, the height of the object, and the gravitational acceleration of the object.

Assuming that the balls are on the Earth, we also know the gravitational acceleration.

$\vec{g}= 9.8m/s^2[down]$

Solution:

Because direction does not matter for the calculation of energy, we will disregard the vector notation.

Case A Case B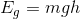

$E_{g}=mgh$

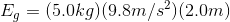
$E_{g}=(5.0kg)(9.8m/s^2)(2.0m)$

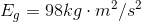
$E_{g}=98kg\cdot m^2/s^2$

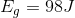
$E_{g}=98J$

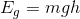
$E_{g}=mgh$

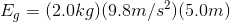
$E_{g}=(2.0kg)(9.8m/s^2)(5.0m)$

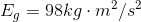
$E_{g}=98kg\cdot m^2/s^2$

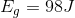
$E_{g}=98J$

Paraphrase:

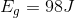
Both the 5.0 kg bowling ball suspended 2.0 m above the floor, and the 2.0 kg cinder block suspended 5.0 m above the floor, have the same amount of gravitational potential energy: $E_{g}=98J$

Case A	Case B
m = 5.0 kg	m = 2.0 kg
h = 2.0 m	h = 5.0 kg

Case A	Case B
$E_{g}=mgh$ $E_{g}=(5.0kg)(9.8m/s^2)(2.0m)$ $E_{g}=98kg\cdot m^2/s^2$ $E_{g}=98J$	$E_{g}=mgh$ $E_{g}=(2.0kg)(9.8m/s^2)(5.0m)$ $E_{g}=98kg\cdot m^2/s^2$ $E_{g}=98J$

At the top of its run, a roller coaster car (of mass 535 kg) has a gravitational potential energy of 393 225 J. What is the height of the car at that point?

Solution

Given:

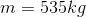
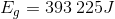
$E_{g}=393 \: 225J$

Required:

We are asked to determine the height of the roller coaster car, based on its mass and gravitational potential energy.

h=?

Analysis:

Gravitational potential energy is proportional to the mass of the object, the height of the object, and the gravitational acceleration of the object.

Assuming that the roller coaster is on the Earth, we also know the gravitational acceleration.

$\vec{g}= 9.8m/s^2[down]$

Because direction does not matter for the calculation of energy, we will disregard the vector notation.

Solution:

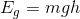
$E_{g}=mgh$

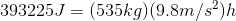
$\frac{393225J}{(535kg)(9.8m/s^2)}=h$

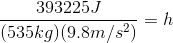
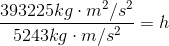
$\frac{393225kg\cdot m^2/s^2}{5243kg\cdot m/s^2}=h$

$75m=h$

Paraphrase:

A roller coaster car that has a mass of 535 kg and a gravitational potential energy of 393 225 J must be 75 m above the ground.

If you double the mass of an object, do you double its gravitational potential energy? Demonstrate your reasoning with a calculation.

Solution

Let’s create an example that will test whether or not doubling an object’s mass will double its gravitational potential energy.

Given:

A bird of mass 10 kg (chosen randomly)

A bird of mass 20 kg (double the mass of the 10 kg bird)

A height of 3 m above the ground (also chosen randomly)

Required:

We are looking to determine the gravitational potential energy of the birds.

$E_{g}=?$

Analysis:

Gravitational potential energy is proportional to the mass of the object, the height of the object, and the gravitational acceleration of the object.

Assuming that the birds are on the Earth, we also know the gravitational acceleration.

$\vec{g}= 9.8m/s^2[down]$

Because direction does not matter for the calculation of energy, we will disregard the vector notation.

Solution:

For the first bird:

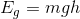
$E_{g}=mgh$

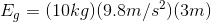
$E_{g}=(10kg)(9.8m/s^2)(3m)$

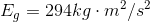
$E_{g}=294kg\cdot m^2/s^2$

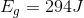
$E_{g}=294J$

For the second bird:

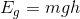
$E_{g}=mgh$

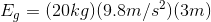
$E_{g}=(20kg)(9.8m/s^2)(3m)$

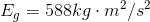
$E_{g}=588kg\cdot m^2/s^2$

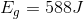
$E_{g}=588J$

Comparing the two gravitational potential energies:

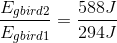
$\frac{E_{g bird2}}{E_{g bird1}}=\frac{588J}{294J}$

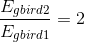
$\frac{E_{g bird2}}{E_{g bird1}}=2$

Paraphrase:

When the mass of an object is doubled (but its height remains the same), the gravitational potential energy of the object also doubles. This makes sense, as gravitational potential energy is directly proportional to the mass of the object.

Kinetic Energy

Another type of energy for which we can derive the equation is kinetic energy: the energy possessed by an object due to its motion. Though there can be different kinds of kinetic energy based on what is doing the moving (for instance, thermal energy is the energy an object has due to the movement of its particles), for now we will focus on an entire object moving, like a bird flying, or a football player running.

Just like with gravitational potential energy, we start with our equation for work.

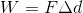
$W= F\Delta d$

Remembering that work is a change in energy, we can replace the W symbol with a symbol representing the change in energy due to the motion of an object: 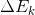$\Delta E_{k}$ .

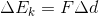
$\Delta E_{k}=F\Delta d$

In this case, and unlike with gravitational potential energy, we don’t know what force or forces are being applied to our object. There is likely an applied force of some sort, but there could be a tension force, or even a friction force. The best we can do is replace the force in the equation with our equation for net force: Newton’s second law.

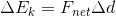
$\Delta E_{k}=F_{net}\Delta d$

...and since 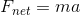$F_{net}=ma$ , we can write:

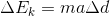
$\Delta E_{k}=ma\Delta d$

Note that we are only dealing with the magnitudes of these values, and hence have removed all vector notation.

Now, we have to think back to kinematics to come up with a simplification for this equation. If we rearrange the equation for average velocity,

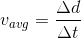
$v_{avg}=\frac{\Delta d}{\Delta t}$

… we can solve for 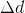$\Delta d$ and write:

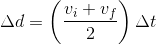
$\Delta d=\left ( \frac{v_{i}+v_{f}}{2} \right )\Delta t$

Click here to see the details of this step.

Another way of writing average velocity is

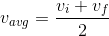
$v_{avg}=\frac{v_{i}+v_{f}}{2}$

This makes sense, as the way we find the average for any group of measurements is to add them all, and then divide the sum by the total number of measurements. In kinematics, there is an additional condition that must be true for this simple relation to hold: the object must be experiencing uniform (constant) acceleration. It does not apply to situations where the acceleration of the object is changing over time.

As these are both equations for average velocity, we can set them equal to each other:

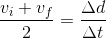
$\frac{v_{i}+v_{f}}{2}=\frac{\Delta d}{\Delta t}$

Solving for $\Delta d$ requires multiplying both sides of the equation by 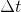$\Delta t$ which leaves us with:

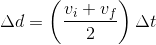
$\Delta d=\left ( \frac{v_{i}+v_{f}}{2} \right )\Delta t$

Let’s now take a look at another equation from kinematics. Remember that acceleration is the change in velocity over the change in time. Again, we are only looking at the magnitudes of these values, so we have removed the vector notation.

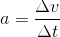
$a=\frac{\Delta v}{\Delta t}$

The change in velocity can be written as 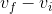$v_{f}-v_{i}$

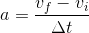
$a=\frac{v_{f}-v_{i}}{\Delta t}$

...and we can rearrange this to solve for the change in time:

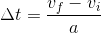
$\Delta t=\frac{v_{f}-v_{i}}{a}$

We can then substitute this value of Δt into our equation above for Δd:

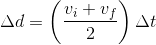
$\Delta d=\left ( \frac{v_{i}+v_{f}}{2}\right )\Delta t$

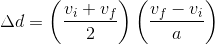
$\Delta d=\left ( \frac{v_{i}+v_{f}}{2}\right )\left ( \frac{v_{f}-v_{i}}{a}\right )$

Multiplying the fractions together gives us:

$\Delta d= \frac{v^2_{f}-v^2_{i}}{2a}$

Click here to see the details of this step.

When multiplying fractions, we multiply the numerators together, and then multiply the denominators together.

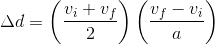
$\Delta d=\left ( \frac{v_{i}+v_{f}}{2}\right )\left ( \frac{v_{f}-v_{i}}{a}\right )$

$\Delta d=\frac {\left (v_{i}+v_{f} \right )\left ( v_{f}-v_{i} \right )}{2a}$

Using the distributive property, we can expand the brackets in the numerator:

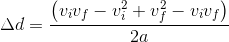
$\Delta d=\frac {\left (v_{i}v_{f}-v^2_i+v^2_f- v_{i}v_{f}\right )}{2a}$

Simplifying the numerator, we get:

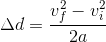
$\Delta d= \frac{v^2_{f}-v^2_{i}}{2a}$

Multiplying both sides by a gives us:

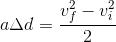
$a\Delta d=\frac{v^2_f-v^2_i}{2}$

So, where does this get us? Take a look back at our original equation for change in kinetic energy. We had stopped at

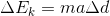
$\Delta E_k=ma\Delta d$

We now have an equation that we can substitute in for 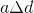$a\Delta d$ .

This leaves us with:

$\Delta E_k=m\left ( \frac{v^2_f-v^2_i}{2} \right )$

Rearranging just slightly to move the constant (½) to the front of the expression, we are left with:

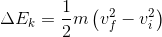
$\Delta E_k=\frac{1}{2}m\left ( v^2_f-v^2_i \right )$

Same as with gravitational potential energy, this is the change in energy an object has as it goes from a slow speed (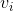 v_i ) to a faster speed ( 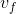v_f ). Though we don’t know what the final speed will be (that will depend on the question), we can set the initial speed to be when the object is at rest: 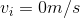v_i=0m/s . Our equation then becomes:

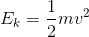
$E_k=\frac{1}{2}m v^2$

Notice again that we removed the Δ from the energy - we are now calculating the amount of energy the object has while travelling at a certain speed, and not the change in energy as the object gains or loses speed.

Looking at the equation, we know that the kinetic energy of any object depends on two things:

The mass of the object, measured in kg;
The speed of the object, measured in m/s.

Practice

Let’s practice with this equation a bit. Try each question, and then check your answer against the solution provided.

Which has more kinetic energy: a 5.0 kg bowling ball suspended rolling at a speed of 2.0 m/s, or a 2.0 kg cinder block being dragged at a speed of 5.0 m/s? How do you know?

Solution

Given:

Case A Case B

m = 5.0 kg

v = 2.0 m/s

m = 2.0 kg

v = 5.0 m/s

Required:

In both cases, we are asked to determine the kinetic energy, so that we can compare the two values.

Analysis:

Kinetic energy is proportional to the mass of the object and the square of the speed of the object.

Solution:

Case A Case B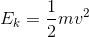

$E_k=\frac{1}{2}mv^2$

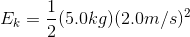
$E_k=\frac{1}{2}(5.0 kg)(2.0m/s)^2$

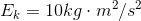
$E_k=10 kg\cdot m^2/s^2$

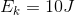
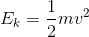
$E_k=\frac{1}{2}mv^2$

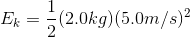
$E_k=\frac{1}{2}(2.0 kg)(5.0m/s)^2$

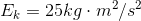
$E_k=25 kg\cdot m^2/s^2$

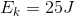
Paraphrase:

The 5.0 kg bowling ball moving at 2.0 m/s has less kinetic energy than the 2.0 kg cinder block moving at 5.0 m/s.

Case A	Case B
m = 5.0 kg v = 2.0 m/s	m = 2.0 kg v = 5.0 m/s

Case A	Case B
$E_k=\frac{1}{2}mv^2$ $E_k=\frac{1}{2}(5.0 kg)(2.0m/s)^2$ $E_k=10 kg\cdot m^2/s^2$	$E_k=\frac{1}{2}mv^2$ $E_k=\frac{1}{2}(2.0 kg)(5.0m/s)^2$ $E_k=25 kg\cdot m^2/s^2$

Niamh kicks a 0.43 kg soccer ball, giving it a kinetic energy of 38.6 J of kinetic energy. What is the speed of the ball?

Solution

Given:

m = 0.43 kg

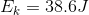
Required:

We are asked to determine the speed of the ball.

v = ?

Analysis:

Kinetic energy is proportional to the mass of the object and the square of the speed of the object.

Solution:

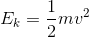
$E_k=\frac{1}{2}mv^2$

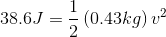
$38.6J=\frac{1}{2}\left ( 0.43 kg \right )v^2$

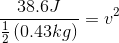
$\frac{38.6J}{\frac{1}{2}\left ( 0.43 kg \right )}=v^2$

$\frac{38.6kg\cdot m^2/s^2}{0.215kg}=v^2$

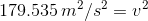
$179.535\, m^2/s^2=v^2$

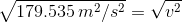
$\sqrt{179.535\, m^2/s^2}=\sqrt{v^2}$

$13.4\: m/s=v$

Paraphrase:

When Niamh kicked the ball, she made the ball travel at a speed of 13.4 m/s.

If you double the speed of an object, do you double its kinetic energy? Demonstrate your reasoning with a calculation.

Solution

Let’s create an example that will test whether or not doubling an object’s speed will double its kinetic energy.

Given:

A person of mass 60 kg (chosen randomly)

A speed of 5 m/s (also chosen randomly)

A speed of 10 m/s (double the initial speed0

Required:

We are looking to determine the kinetic energy of the person travelling at different speeds.

Analysis:

Kinetic energy is proportional to the mass of the object and the square of the speed of the object.

Solution:

For the person moving at a speed of 5 m/s:

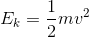
$E_k=\frac{1}{2}mv^2$

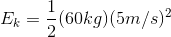
$E_k=\frac{1}{2}(60kg)(5m/s)^2$

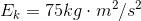
$E_k=75kg\cdot m^2/s^2$

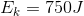
For the same person moving at a speed of 10 m/s:

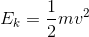
$E_k=\frac{1}{2}mv^2$

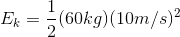
$E_k=\frac{1}{2}(60kg)(10m/s)^2$

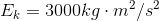
$E_k=3000kg\cdot m^2/s^2$

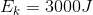
Comparing the two kinetic energies:

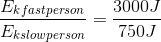
$\frac{E_{kfastperson}}{E_{kslowperson}}= \frac{3000J}{750J}$

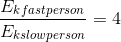
$\frac{E_{kfastperson}}{E_{kslowperson}}= 4$

Paraphrase:

When the speed of an object is doubled (but its mass remains the same), the kinetic energy of the object quadruples (not doubles). This makes sense, as kinetic energy is directly proportional to the square of the speed of the object, which means that as the speed is doubled, the kinetic energy increases by a factor of .

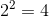Reflection

This is an image of a person holding a ball, preparing to drop it.

Take a look around you. Pick up a non-breakable object, and hold it at shoulder height above the ground. As you do so, consider the object’s gravitational potential and kinetic energies. You may not have the numbers to perform the calculations, but you should have an idea of whether or not the object currently has both of those energies (hint: the object only has one).

Now drop the object. As it falls to the floor, observe and reflect on what is happening to the object’s kinetic energy and gravitational potential energy. Are they changing as the object falls? If so, how?

Finally, though you cannot freeze the object in place just before it hits the floor, give some thought as to what the object’s kinetic and gravitational potential energies are at the split second before it bounces (or smashes).

Create a reflection to answer the following questions:

What happens to the height of the object as it falls?
Knowing what you know about the height, when does the object you’re dropping have the GREATEST gravitational potential energy? When does it have the LEAST gravitational potential energy?
What happens to the speed of the object as it falls?
Knowing what you know about the speed, when does the object have the GREATEST kinetic energy? When does it have the LEAST kinetic energy?
Where do you think the object gets its energy from in order to move faster as it falls?

Go To Portfolio

That last question is tricky. You likely saw that the object sped up as it fell (unless you were in a microgravity environment). As it travelled at faster and faster speeds, it gained kinetic energy. But where does that energy come from? For that matter, where does any energy come from?

The answer turns out to be quite simple: energy of a given type always comes from some other form of energy. This is a fundamental principle of physics known as the conservation of energy: energy cannot be created or destroyed, only transformed from one type to another.

(Upon learning this, one often asks where the very first energies in the universe came from. That is a problem cosmologists are currently trying to solve!)

When an object falls toward the ground, it “loses” gravitational potential energy as its height decreases, and “gains” kinetic energy as its speed increases. In reality, it is neither gaining nor losing energy: as the object falls, its gravitational potential energy is transformed into kinetic energy.

At any point in time as the object falls, it has what is called total mechanical energy (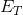 E_T ): the total of kinetic energy AND gravitational potential energy combined. We can write this as:

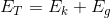
E_T=E_k+E_g

Throughout the object’s fall, even though its kinetic energy will change and its gravitational potential energy will change, its total mechanical energy will stay the same.

Reflection

Watch the following video and reflect on the questions below.

In the video, you’ll notice that the gravitational potential energy at the top of the hill is equal to the kinetic energy at the bottom of the hill. If the roller coaster is stopped at any point along its path, what do you notice about the sum of the gravitational potential energy and kinetic energy. Whenever the roller coaster is stopped, is the mechanical energy always the same?

Where is the gravitational potential energy and the kinetic energy exactly the same? Does this location make sense? Why?

Go To Portfolio

As we saw in the simulation, if we know the amount of gravitational potential energy an object has at the top of its fall (by measuring the object’s height and mass), we automatically know the amount of kinetic energy at the bottom. Because we already know the mass, we can use the formula for kinetic energy to calculate the object’s speed.

Example

A piano of mass 150 kg is pushed out a fourth storey window (12 m high). What will its speed be just before it hits the ground?

Given:

m = 150 kg

h = 12 m

Required:

We are asked to determine the speed of the piano at the end of its fall.

v = ?

Analysis:

Total mechanical energy is the sum of the gravitational potential energy (which is proportional to the mass of the object, the height of the object, and the gravitational acceleration of the object) and the kinetic energy (which is proportional to the mass of the object and the square of the speed of the object).

At the top of the fall, the piano is stationary, so v = 0 m/s.

At the bottom of the fall, the height of the piano is 0 m.

Assuming that the piano is on the Earth, we also know the gravitational acceleration.

$\vec{g}= 9.8m/s^2[down]$

Because direction does not matter for the calculation of energy, we will disregard the vector notation.

Solution:

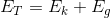
E_T=E_k+E_g

At the top of the piano’s fall:

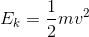
$E_k=\frac{1}{2}mv^2$

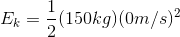
$E_k=\frac{1}{2}(150kg)(0m/s)^2$

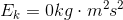
$E_k=0kg\cdot m^2s^2$

E_k=0J

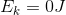
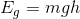
$E_{g}=mgh$

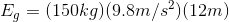
E_g=(150kg)(9.8m/s^2)(12m)

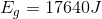
E_g=17640J

So at the top:

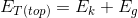
$E_{T(top)}=E_k+E_g$

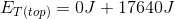
$E_{T(top)}=0J+17640J$

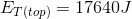
$E_{T(top)}=17640J$

Since 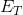E_T at the top of the piano’s fall is equal to 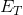E_T at the bottom of its fall,

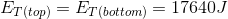
$E_{T(top)}=E_{T(bottom)}=17640J$

So at the bottom, we can write:

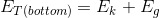
$E_{T(bottom)}=E_k+E_g$

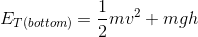
$E_{T(bottom)}=\frac{1}{2}mv^2+mgh$

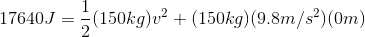
$17640J=\frac{1}{2}(150kg)v^2+(150kg)(9.8m/s^2)(0m)$

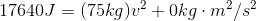
$17640J=(75kg)v^2+0kg\cdot m^2/s^2$

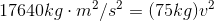
$17640kg\cdot m^2/s^2=(75kg)v^2$

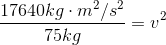
$\frac{17640kg\cdot m^2/s^2}{75kg}=v^2$

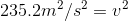
235.2m^2/s^2=v^2

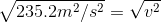
$\sqrt{235.2m^2/s^2}=\sqrt{v^2}$

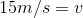
15m/s=v

Paraphrase:

A 150 kg piano dropped from a height of 12 metres will be travelling at a speed of 15 m/s just before it hits the ground.

Lab: Conservation of Energy

In this task, we will verify the conservation of energy principle.

You will do this by rolling an object down a ramp, and compare its energy at the top of the ramp to its energy at the bottom of the ramp. It is up to you to choose which object you use (make sure they can roll, like a ball, a soup can, or a toy car), the height from which you start it rolling down the ramp, and how you will measure the time it takes for the object to roll the entire length of the ramp.

For this investigation, you will be prompted for most parts, and even given some of the wording. In this task, anything in italics must be answered or completed; anything in regular type can be copied directly. Check with your teacher if you have any questions.

Read through the lab instructions below, and develop a procedure. Once your teacher has approved your procedure, complete the inquiry, and submit the required parts below.

Purpose: The purpose of this lab is to… What is the purpose of this investigation? What are we trying to prove?

Hypothesis: How do you think the energy at the top of the ramp will compare with the energy at the bottom of the ramp? Why do you think this?

Materials: Read through the observations and analysis sections to determine what materials you might need. Make a complete list of all the materials you use to collect your data.

Procedure: Read through the observations and analysis sections to determine what information you will need to collect, and then write a procedure for the investigation. Don’t forget to include how the timing was accomplished, and how certain variables (such as height, starting time, etc.) were controlled.

If someone was to reproduce this exact experiment, what would they need to know? Be sure your procedure is in past tense (use the passive voice). Be sure the procedure you create is safe.

Observations:

Record the following information as you perform the experiment:

The vertical distance from the top of the ramp to the floor (in metres);
The mass of your object (in kilograms);
The length of the ramp (in metres);
The time it takes for the object to roll down the entire length of the ramp (in seconds);
- You may wish to collect this piece of data several times to later determine an average time.

Analysis:

Calculate the gravitational potential energy the object has when it is at the top of the ramp.
Determine the average time the object takes to roll down the ramp.
Determine the average speed of the object as it rolled down the ramp (HINT: you know both the distance the object rolled, as well as how long it took, on average).
Double your average speed in order to determine the final speed of the object at the bottom of the ramp. This can be done because:

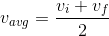
$v_{avg}=\frac{v_i+v_f}{2}$

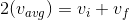
$2(v_{avg})=v_i+v_f$

...and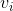 is zero (assuming you started the object from rest).
Determine the kinetic energy the object has at the bottom of the ramp.
Compare the kinetic energy of the object at the bottom of the ramp to the gravitational potential energy of the object at the top of the ramp. This is known as the efficiency:

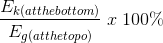
$\frac{E_{k(at the bottom)}}{E_{g(at the topo)}} \; x\; 100\%$
Was the conservation of energy principle upheld? If not, why do you think this is?

Conclusion: In one or two sentences at most, summarize your findings.

Double check the rubric to make sure you have everything you need, and then submit your work to your teacher.

Submit Your Work

In an ideal world, one hundred percent of the object’s gravitational potential energy at the top of its fall gets transformed into kinetic energy just before it hits the ground. In reality, though, some of the energy is transformed into other types. In the investigation you just performed, could you hear the object as it rolled down the ramp? If so, some of the initial gravitational potential energy was transformed into sound energy instead of kinetic energy.

This is an image of a thermometer, which is used to measure the average kinetic energy of a substance, otherwise known as thermal energy.

If not all of the gravitational potential energy is transforming into kinetic energy, there is a decrease in efficiency. One of the most common energy transformations that lead to decreased efficiency is the work done by the force of kinetic friction which transforms mechanical energy into thermal energy.

Thermal energy is measured by temperature (which is actually a measurement of the average kinetic energy of a substance’s particles). The transfer of thermal energy occurs in the form of heat. If there is an increase in temperature as two objects rub against each other, energy is being transformed (usually in a non-useful way).

In our original roller coaster example, not all of the energy gained by starting at the top of that first hill gets turned into kinetic energy at the bottom (though most of it does). Some energy gets lost as sound (the sound of the wheels against the track), yet more energy gets lost as heat due to the friction between the wheels and the track, or between the wheels and the axles.

Another example is close at hand: if you were to rub your hands together vigorously, some of the energy you put into moving your hands is lost as sound (you can hear your hands as they rub together), but also as thermal - you can feel the increase in temperature between the palms of your hands.

CONSOLIDATION

Summary

Gravitational potential energy is the energy stored in a object due to its height above the ground. It depends on the mass of the object, the gravitational acceleration due to the Earth, and the height of the object.

E_g=mgh

Kinetic energy is the energy possessed by an object due to its motion. It depends on the mass of the object, measured in kg, and the speed of the object, measured in m/s.

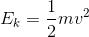
$E_k=\frac{1}{2}mv^2$

Total mechanical energy is the sum of the gravitational potential energy of the object and the kinetic energy of the object.

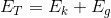
E_T=E_k+E_g

Conservation of energy is a fundamental principle in physics that states energy cannot be created or destroyed, only transformed from one type to another.

Thermal energy is the energy possessed by an object whose particles are moving. These moving particles will spontaneously transfer some of their energy to cooler objects nearby; we perceive this transfer of thermal energy as heat. If there is an increase in temperature as two objects rub against each other, energy is being transformed into thermal energy.

Reflection

Review the content of your reflections and add any additional thoughts to your notes. What three items do you believe are the most significant things you have learned in this activity?

What questions do you have about this content? What are you still wondering? Take the time to discuss your progress with your teacher and answer any questions you might still have.

Go To Portfolio

Work, Energy, and PowerKinetic Energy, Gravitational Potential Energy, and Thermal Energy

MINDS ON

Reflection

ACTION

Gravitational Potential Energy

Practice

Solution

Solution

Solution

Kinetic Energy

Practice

Solution

Solution

Solution

Reflection

Reflection

Example

Lab: Conservation of Energy

CONSOLIDATION

Summary

Reflection

Work, Energy, and Power
Kinetic Energy, Gravitational Potential Energy, and Thermal Energy