Simple Machines
Efficiency of Simple Machines

MINDS ON

Programmable Thermostats

A programmable thermostat like the one shown, is designed to adjust the temperature of your home according to pre-set temperatures programmed throughout the day. They are designed to reduce the amount of “wasted energy” you use to control the temperature in your home. They can be programmed to decrease the temperature of your home during the winter months while you are at school or at work and then gradually increase the temperature just as you are expected to be home. The same holds true for warmer seasons; the thermostat can be programmed to increase the temperature of your home while you are at school or at work, and then gradually decrease the temperature just as you are expected to be home.

This image depicts a renewable energy concept of a miniature house with a digital programmable thermostat and a solar panel sitting on the roof.

Programmable thermostats can be used in many facilities, such as, places of business, recreation facilities, universities and colleges, and even industrial factories and manufacturing facilities.

Reflection

Create a reflection to answer the following questions:

How would you adjust a programmable thermostat throughout the year?
Programmable thermostats are designed to “reduce the amount of wasted energy” in your home. Explain what you think this means and the types of energies it is referring to.
What conclusion does the artist want you to draw from the solar panel sitting on the roof of the house in this picture?

Go To Portfolio

Watch the video below entitled One Nature produced by The David Suzuki Foundation and make note of the various Canadian artists, poets, scientists, explorers, humanitarians, athletes, and aboriginal leaders in the video. As you watch, reflect upon the message that they are trying to impart upon you and the significant role you play in this world and how the words climate change, global warming, renewable energy, and machine efficiency tie into their message.

ACTION

Efficiency of a Simple Machine

Recall!

The actual mechanical advantage (AMA) of a machine is determined by the ratio of the output forces (load forces) to the input forces (effort forces) and is mathematically represented by the equation,

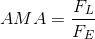
$AMA=\frac{F_{L}}{F_{E}}$

It takes into account the energy losses, often referred to as “waste energy” caused by friction and normal wear and tear of the machine’s parts.

The ideal mechanical advantage (IMA) of a machine is determined by the ratio of the physical parts of the machine (i.e. load arms and effort arms) and is mathematically represented by the equation,

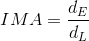
$IMA=\frac{d_{E}}{d_{L}}$

The IMA is also referred to as the “theoretical mechanical advantage” because it represents the maximum mechanical advantage of a machine that does not experience energy losses (i.e. waste energy or energy that is not useful) caused by friction or normal wear and tear of the machine’s parts.

The AMA and the IMA is analogous to marks you earn on a test and the total amount of marks that the test is out of. Through this analogy, the IMA represents the maximum amount of marks you “should” earn on the test and the AMA represents the total amount of marks you “do” earn on a test.

Your teacher can determine the depth of your knowledge or how efficient you are at explaining and demonstrating your understanding by calculating the ratio of the total amount of marks you “do” earn on a test to the total amount of marks you “should” earn and multiply this number by 100. The number you calculate is a number that is out of 100 or often reported as a percentage (%).

Much like you can calculate the efficiency of your knowledge or understanding on a certain test, you can also calculate the efficiency of a machine by calculating the ratio of the actual mechanical advantage (i.e. “do”) to the ideal mechanical advantage (i.e. “should”) and multiply this number by 100.

The efficiency of a machine can be represented mathematically by the following equation:

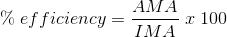
$\%\; efficiency=\frac{AMA}{IMA}\; x\; 100$

Efficiency of the Human Body

This image depicts an image of the internal components of the human body made up of gears, pulleys, wheels and axles, and levers.

This image depicts the internal components of the human body as a compound machine made up of many levers, pulleys, gears, and wheel and axles. Although, this depiction seems slightly unrealistic, the concept draws from a thorough understanding of biomechanics and the various biological simple machines that make up this complex, dynamic, compound machine we know as the human body.

As great as our human body seems, in comparison to other living organisms on our planet Earth, it is, scientifically quite inefficient. One of the most distinct features of modern humans (i.e. homo sapiens) is the size of our brains. Unlike plants, humans must ingest food to get energy and convert the chemical potential energy in the food to more usable forms, such as kinetic, thermal, gravitational potential, and electrical energy to be used by our cells to power our entire biological system. Although the brain is quite small (average mass is 1400 g) compared to other organs in the body, it uses about 20 % of the body’s energy consumption. That’s a lot of food for one organ! The rest of the energy is divided amongst the muscles, biological processes, organs, and cell regeneration to name a few.

Einstein's Brain

This image depicts an illustration of the theoretical physicist, general theory of relativity author, Nobel Prize winner Albert Einstein.

The famous physicist, Albert Einstein, was quoted as stating that he learns better visually rather than verbally. This statement should not come as a shock coming from the individual that visualized and developed some of the most extraordinary physics concepts of the modern era. So significant were they, that we call him the father of modern physics.

When Albert Einstein died in 1955, his brain was removed from his body and studied (without his permission unfortunately). Studies showed that his brain had a mass (about 1230 g) that was slightly below average (about 1400 g) for a person of that time. His brain also contained more glial cells per neuron, which some scientists believe contributed to his increased ability to conduct his “thought experiments.” Because of his above average number of neuron cells, it is assumed that Einstein would require more input energy than the average person in order for his neuron cells to function and make connections. Scientists also noticed that the part of the brain that is responsible for mathematical computations and reasoning seemed to be larger than average in his brain and because of this finding, many scientists believe that this larger portion enabled Einstein’s brain to work more efficiently than average.

One of the most studied biological systems in the world are those of professional athletes such as Olympic athletes (e.g. track and field, swimmers, marathon runners) and professional sport athletes (e.g. baseball, soccer, volleyball). These athletes have bodies that are highly efficient biological systems compared to those of the general population. In other words, their bodies are able to convert chemical potential energy stored in their food more efficiently to electrical and mechanical energy to fuel their brain and muscles to perform their perspective sports at a high level.

Let’s look at your biomechanical system in more depth and learn how to calculate the efficiency of one of the levers in your body.

The Forearm and Triceps

The tricep muscle’s main purpose is to extend and retract the arm at the elbow joint. Most people do not know that the tricep muscle is much bigger than the bicep muscle and therefore, generally stronger as well. For this reason, the tricep muscle plays a bigger role in the mechanics of the body than the biceps do. Then, why do most people train the biceps in the gym more often than the triceps?

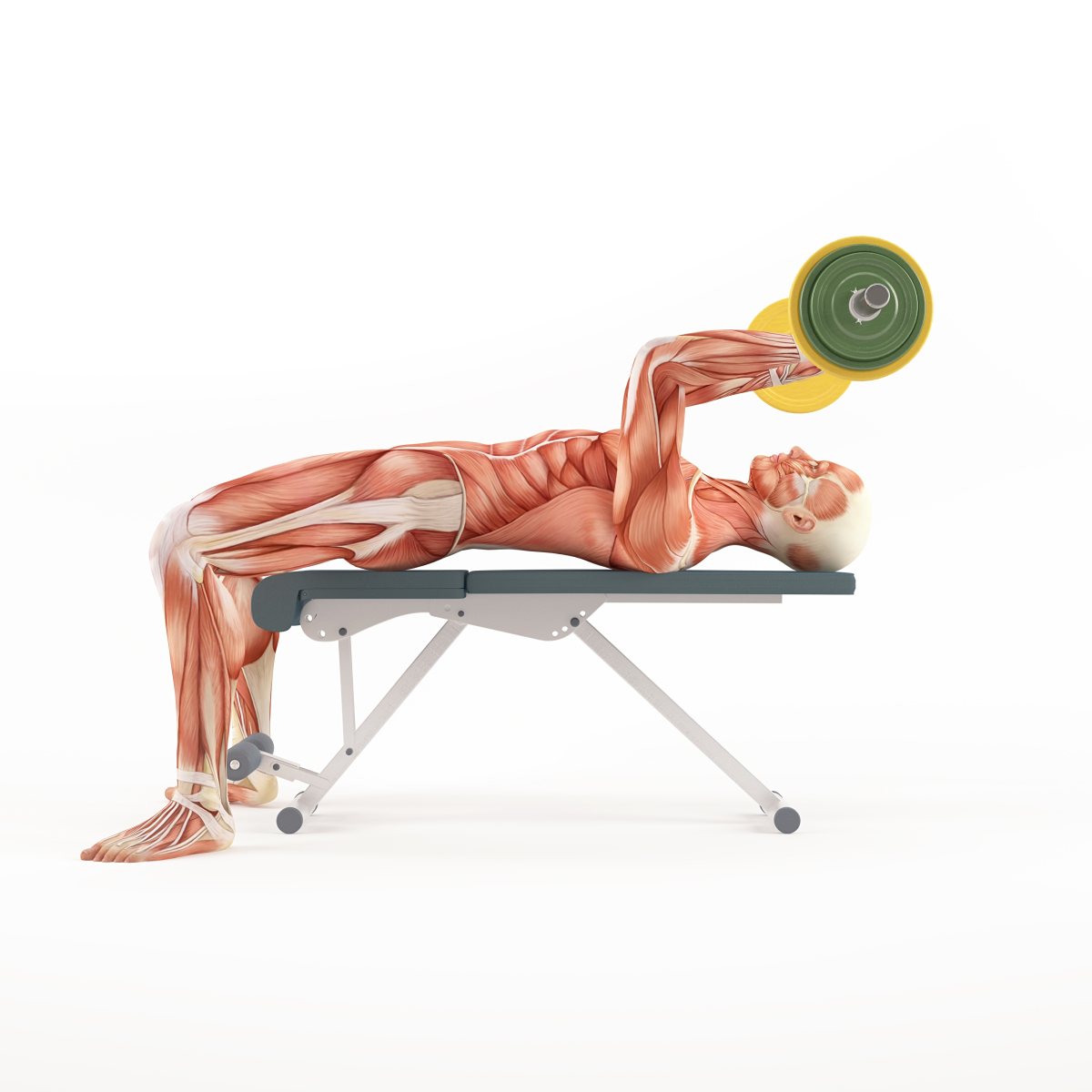
This image depicts an illustration of a human body laying on a workout bench holding a bar with weights over their head at a ninety degree angle. The illustration shows the muscle structures that make up the human body.

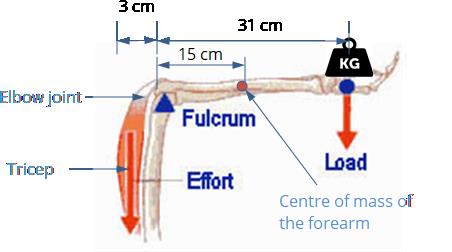
This image depicts a zoomed in and labelled image of the arm when someone is bench pressing weights.

Assume that the mass of 20.0 kg of the weight (bar and weights) is divided evenly between each arm and the mass of the forearm is 2.0 kg is concentrated 15 cm from the elbow joint.

Let’s calculate the actual mechanical advantage of the tricep-forearm system.

Given:

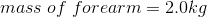
$mass\; of\; forearm=2.0kg$

Required:

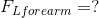
$F_{Lforearm}=?$

Analysis:

The magnitude of the load force due to the weight is equivalent to the magnitude of the force of gravity on the weight.

Solution:

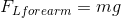
$F_{Lforearm}=mg$

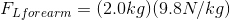
$F_{Lforearm}=(2.0kg)(9.8N/kg)$

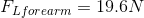
$F_{Lforearm}=19.6N$

Paraphrase:

The magnitude of the load force due to the forearm is 20 N.

Now, let’s calculate the magnitude of the load force due to the mass of the weight. Remember, we are assuming that the weight of the bar and the weights is divided evenly between both arms.

Given:

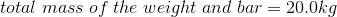
$total\; mass\; of\; the\; weight\; and\; bar=20.0 kg$

Required:

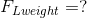
$F_{Lweight}=?$

Analysis:

The magnitude of the load force due to the weight is equivalent to the magnitude of the force of gravity on the weight. Assume that the mass of the bar and weights are divided evenly between each arm.

Solution:

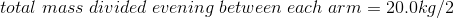
$total\;mass\;divided\;evening\;between\;each\;arm=20.0kg/2$

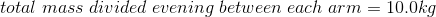
$total\;mass\;divided\;evening\;between\;each\;arm=10.0kg$

$F_{Lweight}=mg$

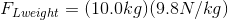
$F_{Lweight}=(10.0kg)(9.8N/kg)$

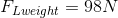
$F_{Lweight}=98N$

Paraphrase:

The magnitude of the load force due to the weight is 98.0 N.

We can now calculate the magnitude of the effort force needed to maintain static equilibrium that prevents the forearm from rotating.

Given:

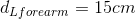
$d_{Lforearm}=15cm$

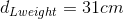
$d_{Lweight}=31cm$

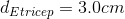
$d_{Etricep}=3.0cm$

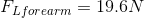
$F_{Lforearm}=19.6N$

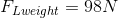
$F_{Lweight}=98N$

Required:

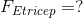
$F_{Etricep}=?$

Analysis:

The law of the lever states that the magnitude of the torque created by the effort force applied an effort arm distance from the fulcrum must equal the magnitude of the torque created by the load force applied a load arm distance from the fulcrum in order to maintain static equilibrium or prevent rotation. This means that the total effort force applied by the triceps must provide enough torque to “balance” the total torque created by the load forces applied by the forearm and weights, in order to prevent rotation and the ability to hold the weight above the head.

Simply stated, the total magnitude of the effort torque must equate to the total magnitude of the load torques.

Solution:

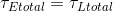
$\tau _{Etotal}=\tau _{Ltotal}$

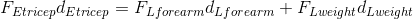
$F_{Etricep}d_{Etricep}=F_{Lforearm}d_{Lforearm}+F_{Lweight}d_{Lweight}$

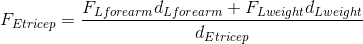
$F_{Etricep}=\frac{F_{Lforearm}d_{Lforearm}+F_{Lweight}d_{Lweight}}{d_{Etricep}}$

$F_{Etricep}=\frac{(19.6N)(0.15m)+(98N)(0.31m)}{(0.030m)}$

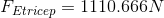
$F_{Etricep}=1110.666N$

Paraphrase:

The magnitude of the effort force needed to maintain static equilibrium and the ability to hold the weight above the head is 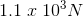$1.1\; x\; 10^3N$ .

Now, calculate the AMA of the tricep-forearm system.

Given:

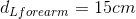
$d_{Lforearm}=15cm$

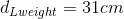
$d_{Lweight}=31cm$

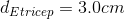
$d_{Etricep}=3.0cm$

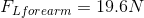
$F_{Lforearm}=19.6N$

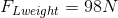
$F_{Lweight}=98N$

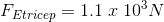
$F_{Etricep}=1.1\; x\; 10^3N$

Required:

AMA=?

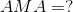
Analysis:

The total load force is the summation of all the load forces that are creating the torque in the clockwise direction.

Solution:

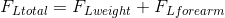
$F_{Ltotal}=F_{Lweight}+F_{Lforearm}$

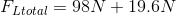
$F_{Ltotal}=98N+19.6N$

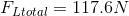
$F_{Ltotal}=117.6N$

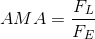
$AMA=\frac{F_{L}}{F_{E}}$

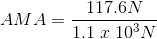
$AMA=\frac{117.6N}{1.1\; x\; 10^3N}$

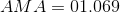
Paraphrase:

The actual mechanical advantage of the tricep-forearm system is 0.11.

Reflection

Create a reflection to answer the following questions related to the tricep-forearm system:

Are you surprised by the calculated result of the actual mechanical advantage? Why or why not? Explain your reasoning.
What would affect the overall mechanical advantage and overall efficiency of the tricep-forearm system?
What changes could this person implement to improve their mechanical advantage and efficiency?
What changes are NOT possible for the person to implement but could also increase their mechanical advantage and efficiency?
What types of sports would benefit from having a high mechanical advantage for the tricep-forearm system. Explain your reasoning.

Go To Portfolio

Wind Turbines

A wind turbine uses the wind, a renewable resource, to transform wind energy (i.e. kinetic energy) to electrical energy. Wind turbines come in many different sizes and vary based on the amount of electricity that they need to produce. They can be designed to create electricity to power a small farmhouse or can be designed to produce electricity that is then passed on to the power grid to be used by small towns or large urban areas.

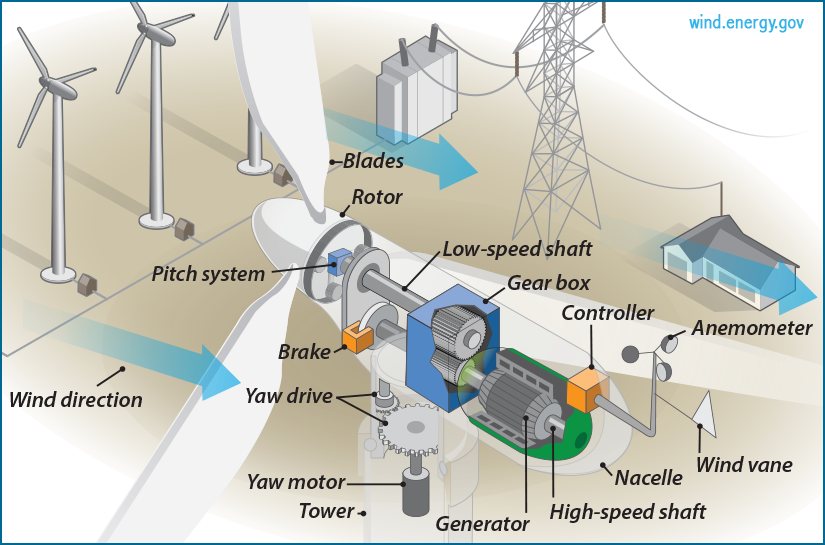
This image depicts a schematic of a wind turbine. — by wind.energy.gov

A wind turbine is made up of three main structures, the propeller-rotor, the nacelle, and the mast or sometimes referred to as the tower. The propeller structure is attached to the nacelle, a housing that contains all the electrical generating components such as the gearbox, drive train, generator, and the brakes. The propeller-rotor and the nacelle all sit atop of the tower.

The kinetic energy of the wind is transformed to kinetic and gravitational potential energy when the wind collides with the propeller-rotor structure and it begins to turn. The kinetic energy of the rotating propellers and rotor is transformed to electrical energy in the generator where it is then used to power various machines and transformed into other types of energies.

Let’s analyze the mechanical advantage and efficiency of one section of an average wind turbine that can be seen along the landscapes of Southwestern Ontario.

This image depicts a schematic of six wind turbines on farmers fields.

Calculate the efficiency of the propeller-rotor and low-speed shaft components if the diameter of the propeller-rotor is 92 m and the radius of the low-speed shaft is 5 m. The AMA is 7.4.

Given:

AMA = 7.4

diameter of the propeller-rotor = 92 m

radius of the low-speed shaft = 5 m

Required:

% efficiency = ?

Analysis:

The propeller-rotor and the low-speed shaft act like a wheel and axle. The wheel, in this case, the propeller-rotor turn the axle, the low-speed shaft. The IMA can be calculated by following the equation for a wheel and axle.

Solution:

To calculate the IMA for a wheel and axle, we must first determine each of their radius.

The radius of the propeller-rotor is half the diameter.

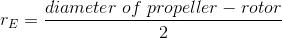
$r_{E}=\frac{diameter\; of\; propeller-rotor}{2}$

$r_{E}=46m$

The IMA of a wheel and axle is determined by the mathematical formula below.

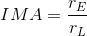
$IMA=\frac{r_{E}}{r_{L}}$

The effort force or input energy is supplied by the propeller-rotor (i.e. wheel) and the load force or the output energy to turn the generator is produced by the low-speed shaft (i.e. axle).

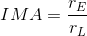
$IMA=\frac{r_{E}}{r_{L}}$

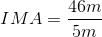
$IMA=\frac{46m}{5m}$

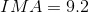
IMA=9.2

If the AMA of the wind turbine in question is 7.4, then the efficiency can be calculated.

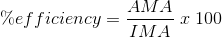
$\%efficiency=\frac{AMA}{IMA}\; x\; 100$

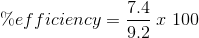
$\%efficiency=\frac{7.4}{9.2}\; x\; 100$

$\%efficiency=80.43\%$

Paraphrase:

The wind turbine is 80% efficient at transforming kinetic energy from the propeller-rotor to the low-speed shaft.

The Efficiency of Wind Turbines

The overall efficiency of a wind turbine is generally around 40 %. Much of the kinetic energy of the wind that is used to rotate the low-speed shaft and the gears of the gearbox that turn the generator is not transformed into useful electrical energy. Most of the kinetic energy is transformed into thermal energy and wasted due to frictional forces in the components contained in the nacelle.

CONSOLIDATION

Summary:

The efficiency of a simple machine can be represented mathematically by the following:

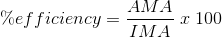
$\%efficiency=\frac{AMA}{IMA}\; x\; 100$

The human body is an example of a biomechanical system.

The efficiency of various levers in a biomechanical system can be determined by calculating the actual mechanical advantage and comparing that to the ideal mechanical advantage.

Thermostats and wind turbines are compound machines that are used to solve current challenges of climate change and global warming.

Simple MachinesEfficiency of Simple Machines

MINDS ON

Programmable Thermostats

Reflection

ACTION

Efficiency of a Simple Machine

Efficiency of the Human Body

Einstein's Brain

The Forearm and Triceps

Reflection

Wind Turbines

The Efficiency of Wind Turbines

CONSOLIDATION

Summary:

Simple Machines
Efficiency of Simple Machines